
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Malynar, 26. ročník - Zimný semester
Vzorové riešenia 1. série nájdeš v časopise Malynar-26-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-26-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 10. október 2016 20:00:00
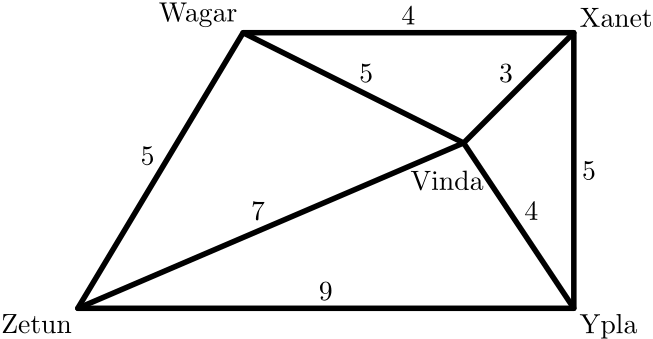
1. Na obrázku sú znázornené obce Zetun, Ypla, Xanet, Wagar, Vinda s uvedenými nákladmi na možné spojenia elektrickým vedením medzi dvomi obcami. Všetkých $5$ obcí má byť spojených jednou súvislou rozvodovou sieťou vedení tak, aby náklady na výstavbu siete boli čo najmenšie. Navrhnite plán tejto siete vedení. Koľko sú celkové náklady na najdrahšiu súvislú rozvodovú sieť so štyrmi vedeniami (navrhnite plán)? Odôvodnite, prečo náklady nemôžu byť väčšie alebo menšie.

2. V zásielke smerujúcej na západ je $40$ modrých, $30$ červených a niekoľko zelených kníh. Žiadna matematická kniha nie je zelená. Všetky červené knihy a polovica modrých kníh sú matematické. Nematematických kníh je dvakrát viac ako matematických. Koľko zelených kníh je v zásielke?
3. Máme trojciferné číslo, ktoré má všetky cifry nepárne. Po pričítaní $421$ má všetky cifry párne. Aké trojciferné čísla majú túto vlastnosť?
4. Päť Indiánov - Medveď, Bizón, Antilopo, Sokol a Jeleň - spomínalo, ako na tábore plnili „bobríka odvahy“. Vedeli, že Jeleň sa vydal na skúšku prvý, ale ďalšie poradie si nepamätali. Každý z nich povedal, na čo si spomenul:
- Medveď: „Nešiel som druhý ani posledný.“
- Bizón: „Ja som taktiež nebol druhý.“
- Antilopo: „Druhý som bol ja.“
- Sokol: „Ja som liezol posledný.“
5. Každá mala jednu veľkú kocku zloženú z $5\times5\times5$ menších kociek. Aby ich vedeli rozoznať, jedna natrela ružovou farbou tri steny svojej kocky a druhá fialovou farbou tiež nejaké tri steny svojej veľkej kocky. Po chvíli sa rozhodli veľké kocky rozobrať. Zistili, že počet malých kociek s aspoň jednou fialovou stenou bol iný, ako počet kociek s aspoň jednou ružovou stenou. Aký bol rozdiel týchto počtov?
6. Doplňte číselnú krížovku (čísla sa dopĺňajú v smere šípok, pričom do štvorčeka patrí vždy práve jedna cifra) tak, aby platili nasledujúce podmienky.
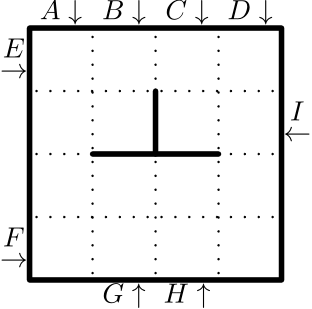
- Žiadne z čísel nemôže začínať nulou.
- Pre každé z čísel $A$, $D$, $E$, $F$ platí, že rozdiel medzi jeho susednými ciframi (v poradí v akom číslo čítame) je rovnaký. Takúto vlastnosť majú napr. čísla $1234$, $8642$, … ale nie číslo $1414$ (lebo rozdiel čísel $1$ a 4, je iný ako čísel $4$ a $1$).
- $C + I = 100$.
- Rozdiel najväčšej a najmenšej cifry čísla $A$ je väčší ako rozdiel najväčšej a najmenšej cifry čísla $E$, ale menší ako rozdiel najväčšej a najmenšej cifry čísla $D$.
- Zápis čísla $G$ je rovnaký ako zápis čísla $H$ odzadu.
- Číslo $B$ je palindróm (to znamená, že sa zľava doprava číta rovnako ako sprava doľava).
- Rozdiel medzi prvými dvoma ciframi čísla $F$ je väčší ako rozdiel medzi poslednými dvoma ciframi čísel $A$ aj $D$.

Vzorové riešenia 1. série nájdeš v časopise Malynar-26-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-26-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 14. november 2016 20:00:00
1. Džastin má $5$ kamarátiek. Každá z nich hovorí výlučne buď pravdu, alebo klame (vždy vo všetkých svojich tvrdeniach). Džastin vie, že iba $1$ z nich hovorí pravdu a ostatné sú klamárky. Na základe ich výpovedí zistite, ktorá to je a koľko má rokov.
- Atlanta: „Viem, že Celesta má $12$ rokov. Žiadne dve z nás nemajú rovnako veľa rokov.“
- Bejby: „Ja mám $8$ rokov. Celesta má $10$, Dakota $12$ a Ebi $9$, no Atlanta mi svoj vek nikdy neprezradila.“
- Celesta: „Bejby je odo mňa o $3$ roky mladšia a Dakota je o $3$ roky staršia. Atlanta určite nikomu nepovedala, koľko má rokov.“
- Dakota: „Ja a Ebi sme rovnako staré, máme $11$ rokov.“
- Ebi: „Celesta má $12$ rokov, Dakota má $12$ rokov a ja mám tiež $12$ rokov.“
2. Ustráchaný Jackie Chan sa bojí o svoju záhradu v tvare obdĺžnika s rozmermi $91\times 49$ m. Potrebuje na múr okolo záhrady namontovať kamery. V každom rohu musí byť kamera a rozostupy medzi každými dvomi susednými kamerami na múre musia byť rovnaké. Koľko najmenej kamier potrebuje kúpiť?
3. V Tokiu sa nachádzajú $2$ trezory plné peňazí, v Nikku ďalšie $4$. Mafia potrebuje do Kyota dopraviť $3$ trezory, do Osaky $2$ a do Hirošimy $1$. Dopravné náklady na prepravu jedného trezora sú uvedené v tabuľke. Určte, medzi ktorými mestami sa má prepraviť koľko trezorov, aby preprava bola čo najlacnejšia.
| Kyoto (3) | Osaka (2) | Hirošima (1) | |
| Tokyo (2) | 120 ¥ | 80 ¥ | 60 ¥ |
| Nikku (4) | 40 ¥ | 160 ¥ | 100 ¥ |
4. Máme $10$ vrecúšok zlaťákov a v každom z nich je aspoň $47$ zlatých mincí. Jeden zo sluhov, ktorý mal na starosť prepravu peňazí, bol zlodej a v jednom vrecúšku z každej mince, ktorá normálne váži $10$ g, obrúsil $1$ g. Máme digitálnu váhu. Na váhu vieme položiť ľubovoľný dostupný počet mincí z ľubovoľného vrecúška. Dokážeme na jedno váženie určiť, z ktorého vrecúška zlodej kradol? Keby táto váha nebola digitálna ale rovnoramenná, koľko by sme potrebovali vážení (podobne, na misky váh vieme položiť ľubovoľný dostupný počet mincí z ľubovoľného vrecúška)?
5. Máme šachovnicu. Na každom políčku je umiestnená figúrka. Figúrky sú očíslované od $1$ po počet políčok na šachovnici. Dajú sa figúrky preusporiadať tak, aby každá figúrka skončila na políčku, ktoré susedí s jej pôvodným políčkom hranou (na jednom políčku nesmie stáť viac ako jedna figúrka)? Ak takéto pre usporiadania existujú pre šachovnice $6\times6$ a $3\times3$, nájdite aspoň jedno. Ak nie, vysvetlite prečo.
6. V krajine je $6$ miest, z toho jedno mesto je hlavné a zvyšných päť je okresných. Mestá na komunikáciu používajú poštové holuby. Na každú dvojicu miest má krajina vyhradeného jedného holuba, bieleho alebo sivého, ktorý pravidelne lieta z jedného mesta do druhého a späť, a zabezpečuje tak komunikáciu medzi danými dvoma mestami. Štát vydal nový zákon, a teda potrebuje správu rozposlať do okresných miest. Využijú všetkých piatich holubov, ktorí lietajú cez hlavné mesto, a pošlú tak správu do všetkých okresných miest. Pre istotu však každé okresné mesto pošle tú istú správu aj zvyšným štyrom okresným mestám. Dokážte, že existujú nejaké $3$ mestá, medzi ktorými preletia iba holuby jednej farby.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...