
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Malynar, 31. ročník - Letný semester
Vzorové riešenia 1. série nájdeš v časopise Malynar-31-5
Vzorové riešenia 2. série nájdeš v časopise Malynar-31-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 4. apríl 2022 20:00:00
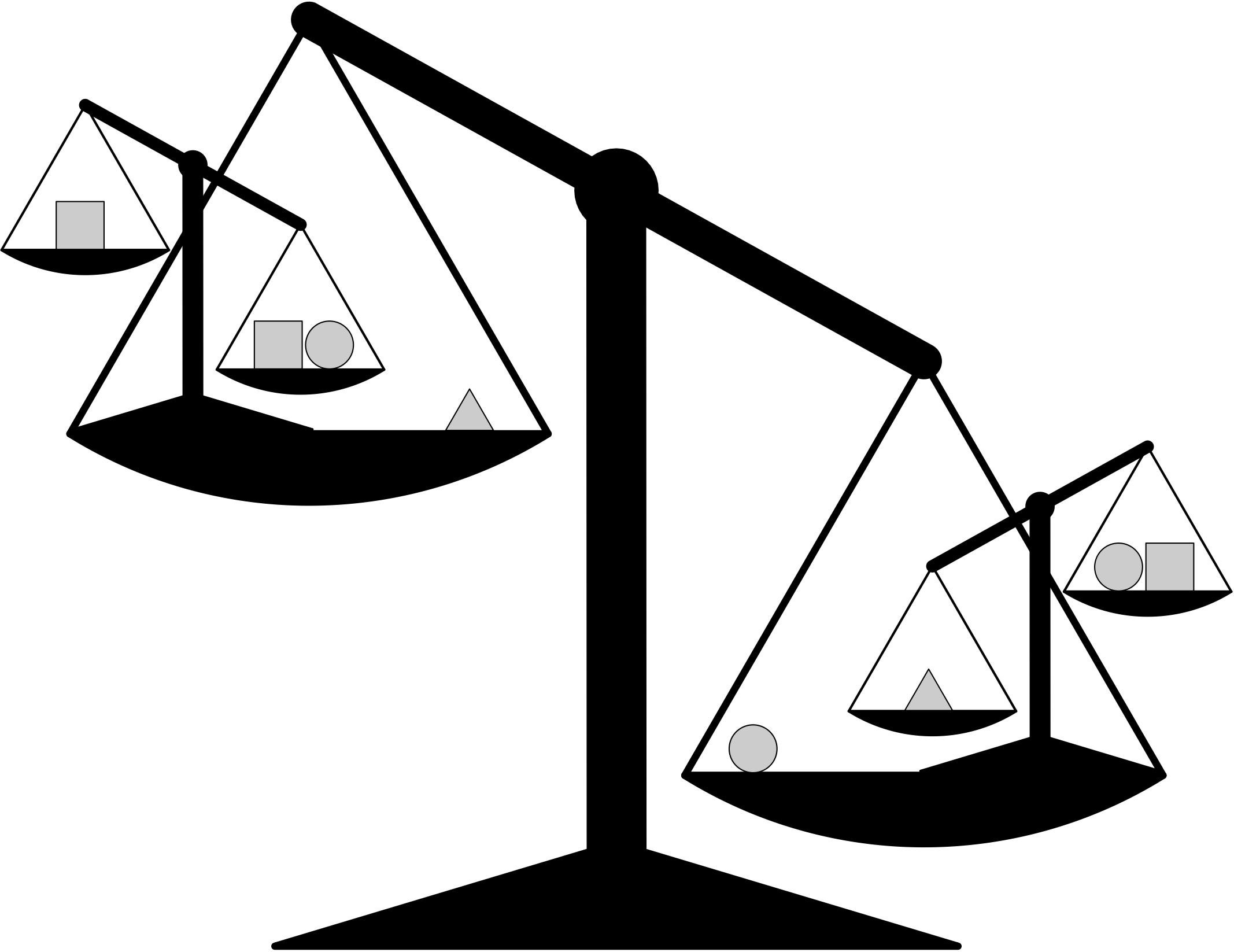
1. Na váhach je tovar v tvare trojuholníkov, štvorcov a kruhov. Platí, že tovar rovnakého tvaru váži vždy rovnako a aj obe malé váhy sú rovnako ťažké. Zoraďte jednotlivé druhy tovaru podľa ich hmotnosti od najťažšieho po najľahší.

2. Len jedno zo siedmich detí hovorí pravdu, a teda aj naozaj vie, čo sa stalo s Juanovou mačičkou. Deti sú postavené v rade vedľa seba. Keď sme sa ich spýtali, ktoré z nich hovorí pravdu, odpovedalo nám len zopár z nich. Tretí chlapec v rade povedal: „Pravdu hovorí buď prvý, alebo druhý.“ Štvrtý povedal: „Ten, ktorý hovorí pravdu, je vedľa mňa.“ Piaty chlapec mu povedal: „Buď pravdu hovorím ja, alebo šiesty chlapec.“ Ktorý z chlapcov hovorí pravdu?
3. Máme trojciferné číslo zložené z troch kartičiek. Následne prehadzovaním kartičiek s ciframi vytvoríme všetky ďalšie trojciferné čísla, ktoré takto vieme dostať. Získame takto práve $3$ nové čísla. Súčet dvoch najmenších z týchto štyroch čísel je $1088$. Aké cifry má pôvodné číslo?
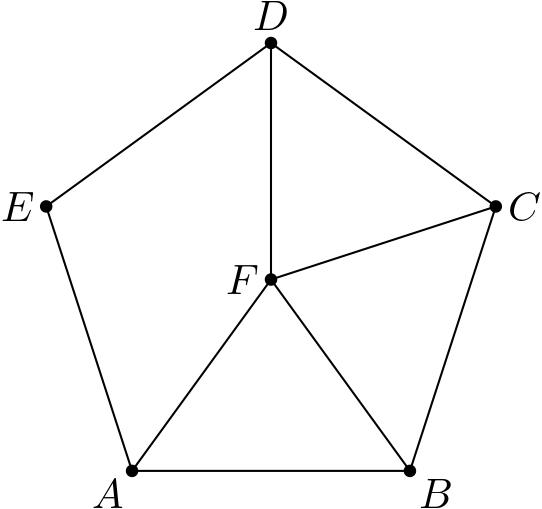
4. V Španielsku majú $6$ miest $A$, $B$, $C$, $D$, $E$ a $F$. Medzi mestami vedú cesty ako na obrázku, každá z nich má nejakú dĺžku v kilometroch (nie nutne celých). Zistite dĺžku cesty medzi $A$ a $E$, ak platí:
- Všetky cesty medzi mestami majú dokopy $30$ kilometrov.
- Ak ideme z mesta $B$ okružnou trasou cez $C$, $D$, $E$, $A$ naspäť do $B$, prejdeme spolu $22$ kilometrov.
- Všetky cesty, ktoré vedú do mesta $F$, sú rovnako dlhé.
- Všetky cesty, ktoré vedú do mesta $C$, majú dokopy dĺžku $14$ kilometrov.
- Cesta medzi $A$ a $B$ je rovnako dlhá ako cesta medzi $D$ a $E$.
- Okružná trasa, ktorá začína aj končí v $A$, a ide postupne cez $F$, $D$, $E$, má dĺžku $11$ kilometrov.

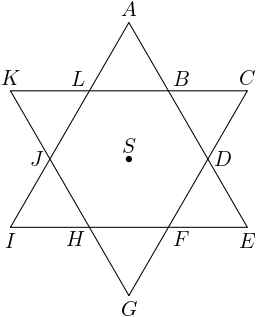
5. Pravidelná šesťcípa hviezda $ABCDEFGHIJKL$ so stredom $S$, ktorá vznikla preložením dvoch rovnakých rovnostranných trojuholníkov ako na obrázku, má obsah $96$ $cm^2$. Platí, že body prieniku $B, D, F, H, J$ a $L$ sú rovnako vzdialené od stredu $S$. Vypočítajte obsah štvoruholníka $ABCF$.

6. Na šachovnici tvaru $25\times 25$ sú umiestnené figúrky, ktoré útočia podľa osobitných pravidiel. Figúrka v bielom poli napáda všetky biele polia v rovnakom riadku a všetky čierne polia v rovnakom stĺpci a figúrka v čiernom poli napáda všetky čierne polia v rovnakom riadku a všetky biele polia v rovnakom stĺpci. Určte maximálny počet figúrok, ktoré je možné umiestniť na hraciu plochu tak, aby sa neohrozovali. Zdôvodnite, prečo sa tam viac figúrok nedá položiť.
Vzorové riešenia 1. série nájdeš v časopise Malynar-31-5
Vzorové riešenia 2. série nájdeš v časopise Malynar-31-6
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 2. máj 2022 20:00:00
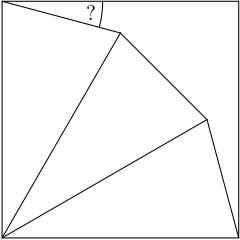
1. Na obrázku je štvorec, v ktorom sa nachádzajú $3$ schody, ktoré mali tvar rovnakých rovnoramenných trojuholníkov. Strany štvorca, ktoré zvierajú uhol hore vpravo, sú steny veže. Aký veľký je uhol medzi bočným schodom a stenou veže?

2. Kúzelník má v krabičke $3$ kartičky, na každej z nich je iná cifra v rozmedzí od $1$ po $9$. Súčet dvoch najmenších dvojciferných čísel, ktoré sa z kartičiek dajú poskladať, je $75$, súčet dvoch najväčších je $170$. Zistite, aké cifry má kúzelník na kartách.
3. V turnaji súťažilo $6$ tímov a každý tím odohral $2$ zápasy s každým iným tímom. Za výhru získal tím $3$ body, za remízu $1$ bod a za prehru $0$ bodov. Prvé $3$ tímy mali rovnako veľa bodov. Aký je najvyšší možný počet, ktorý mohli tieto prvé tri tímy získať? Zdôvodnite, prečo nemohli získať viac bodov.
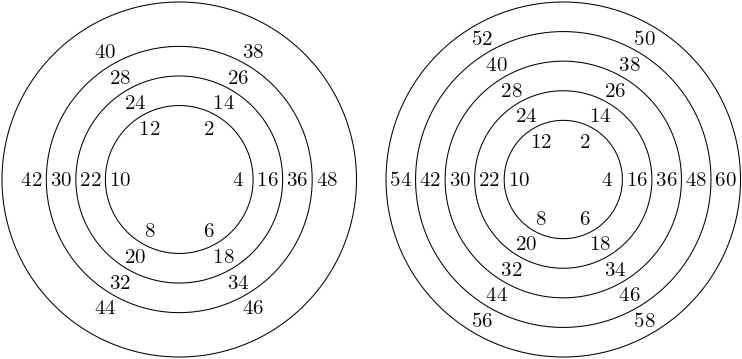
4. Kúzelník má $2$ trezory. Na trezoroch je špeciálny číselný zámok, ktorý sa skladá z otáčateľných kruhových pásov s číslami. Zámok sa otvorí, ak budú čísla usporiadané v šiestich stĺpcoch smerom od stredu a v každom stĺpci bude súčet čísel rovnaký. Dajú sa trezory nižšie otvoriť?

5. Na stole sú $4$ krabice s loptičkami, v každej je na začiatku $10$ loptičiek. Zároveň máme pri stole bazén s neobmedzeným množstvom loptičiek. V každom ťahu môžeme urobiť jeden z troch krokov, ak je možné taký krok urobiť:
- Zobrať z každej krabice $1$ loptičku a hodiť ich do bazéna.
- Vybrať z niektorej krabice $3$ loptičky a rozdeliť ich po $1$ do zvyšných $3$ krabíc.
- Vybrať z bazéna $4$ loptičky a dať $2$ z nich do niektorej krabice a zvyšné $2$ do inej krabice.
6. V kruhu leží niekoľko mincí (viac ako $2$), pričom na začiatku žiadna dvojica susedných mincí nie je otočená rovnako. Ricardo a Hernan sa striedajú v ťahoch. Ten, čo je na rade, musí otočiť súvislý úsek mincí otočených rovnakou stranou nahor susediaci s mincami otočenými naopak. Prehráva ten, po ktorého ťahu sú všetky mince otočené rovnako. Ricardo vyberá, kto bude začínať. Ako si má Ricardo v závislosti od počtu mincí vybrať, aby bez ohľadu na Hernanove ťahy vždy vyhral?
Dodatok pre lepšiu predstavu: Ak by sme mali $10$ mincí rozložených ako na obrázku, potom ten, kto je na ťahu, môže otočiť buď mince $0$, $1$, $2$, $3$, alebo iba mincu $4$, alebo mince $5$ a $6$, alebo mince $7$, $8$ a $9$.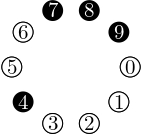
Dodatok pre lepšiu predstavu: Ak by sme mali $10$ mincí rozložených ako na obrázku, potom ten, kto je na ťahu, môže otočiť buď mince $0$, $1$, $2$, $3$, alebo iba mincu $4$, alebo mince $5$ a $6$, alebo mince $7$, $8$ a $9$.

Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...