Počet mojich mincí je $929$-ciferné číslo. Každé dve jeho susedné cifry tvoria dvojciferné číslo, ktoré je násobkom $13$. Posledná cifra počtu je $2$. Aká je jeho prvá číslica?

V meste žije presne $2018$ obyvateľov, ktorí sú postupne očíslovaní od $1$ do $2018$ (každé číslo má práve jeden z obyvateľov). Každý obyvateľ má buď žlté, alebo čierne vlasy. Žltovlasí vždy klamú čiernovlasým a naopak a zároveň ľudia rovnakej farby vlasov si navzájom hovoria pravdu.
Obyvatelia sa postavili do kruhu a každý prehovoril raz k nasledujúcemu človeku podľa poradia ich čísel (prvý k druhému, druhý k tretiemu a tak ďalej, až napokon dvetisícosemnásty k prvému).
Každý z prvých $2016$ ľudí povedal: Človek dve miesta predo mnou má vlasy rovnakej farby ako ja. (Prvý to povedal druhému o treťom, druhý tretiemu o štvrtom atď.)
Človek číslo $2017$ povedal: Prvý človek má vlasy inej farby ako ja.
Posledný človek povedal: Mám žlté vlasy.
Kto má vlasy akej farby?

Kráľ dal každému zo svojich troch synov 4 paličky s dĺžkami 6, 5, 8, 4 dm a povedal im: „Každú zo 4 paličiek môžete najviac raz prepíliť. Urobte to tak, aby ste mi priniesli paličky požadovaných dĺžok.
„Ty, najstarší, Mojmír, prines mi paličky s dĺžkami 2, 2, 3, 4, 4, 4, 5 dm.“
„Ty, stredný, Svätopluk, prines mi paličky s dĺžkami 1, 2, 2, 3, 4, 5, 6 dm.“
„A ty, môj najmladší synček, Predslav voláš sa, prines mi paličky s dĺžkami 1, 1, 1, 2, 3, 3, 4, 4, 4 dm.“
Môže každý zo synov splniť zadanú úlohu? V prípade, že syn dokáže úlohu splniť, nájdite aspoň tri spôsoby, ktorými to dokáže. V prípade, že syn nedokáže úlohu splniť, zdôvodnite prečo.

Záhrada má tvar obdĺžnika, ktorého vrcholy označíme po poradí $A$, $B$, $C$ a $D$. Niekde na strane $AB$ leží bod $E$. Niekde na strane $CD$ ležia body $F$ a $G$ tak, že bod $F$ je k bodu $C$ bližšie ako bod $G$. V trojuholníkoch $AGE$ a $EFB$ sú vysadené žlté narcisy. V trojuholníkoch $BCF$, $FEG$ a $GAD$ sú vysadené červené ruže. Rozhodnite, ktorá z dvoch farieb zaberá v záhrade väčšiu plochu.
Poznámka: Nezabúdajte na to, že presnú polohu bodov E, F a G nepoznáme, a teda úlohu je nutné riešiť všeobecne -- pre všetky možné polohy. Prezradíme tiež, že na riešenie úlohy nie je potrebné žiadne rysovanie.

Ján strieľal do terča, ktorého zasiahnutím mohol získať 30, 12 alebo 6 bodov (za jeden zásah). Vystrelil najviac dvadsaťkrát, pričom každým výstrelom trafil terč. Je zaujímavé, že získal presne sedemnásťkrát viac bodov, ako bol počet jeho výstrelov. Koľko najviac a koľko najmenej bodov mohol Ján získať, keď získal nenulový počet bodov? Koľko zásahov na to potreboval?

Vo vrecúšku bolo 100 loptičiek štyroch farieb. Modrých bolo o toľko menej oproti červeným, ako bolo červených menej oproti žltým. 33 loptičiek sme náhodne vybrali. Medzi vybranými boli všetky zelené, ktoré vo vrecúšku boli, pričom zelená je medzi 100 loptičkami jediná najviac zastúpená farba. Okrem toho sme z každej farby vytiahli aspoň jednu loptičku a vytiahli sme trikrát viac červených ako modrých. Žltých sme vytiahli rovnaký počet ako modrých. V celom vrecúšku (medzi všetkými 100 loptičkami) je červených a žltých loptičiek dokopy viac ako zelených a modrých spolu. Koľko bolo v nádobe akých loptičiek a koľko akých sme vytiahli?

$27$ vojakov bolo ubytovaných v izbách s tromi alebo štyrmi lôžkami, jazdci zvlášť a pešiaci zvlášť. Nájdite všetky možnosti, ako mohli byť vojaci do izieb rozdelení, keď boli všetky izby obsadené úplne. Trojlôžkových izieb bolo obsadených viac ako štvorlôžkových, pričom štvorlôžková izba bola obsadená aspoň jedna. Jazdcov bolo aspoň $10$ a pešiakov bolo viac ako jazdcov.

Súčet trojciferného čísla $\overline{AAA}$ a dvojciferného čísla $\overline{BB}$ je číslo $\overline{CD6E}$. $A$, $B$, $C$, $D$ a $E$ sú rôzne cifry. Zistite, aké hodnoty majú $A$, $B$, $C$, $D$ a $E$

Vojislav ukladá kamienky na niektoré políčka tabuľky $3\times3$ (na jednom políčku môže byť aj viac kamienkov). Potom si spočíta počet kamienkov v každom zo stĺpcov aj riadkov. Chce ich uložiť tak, aby bol každý z týchto šiestich súčtov iný. Koľko najmenej kamienkov musí použiť? Ako napríklad ich môže poukladať?

Rozhodnite, na koľko najmenej rezov viete cukrový kváder $10\times8\times5$ rozplíliť, aby ste z neho mali kocky $1\times1\times1$. Jedným rezom viete rozpíliť súčasne aj viac oddelených telies.

Chceme z $25$ pretekárov vybrať $3$ najrýchlejších, ale nemáme stopky. Na okruhu môže naraz súťažiť maximálne $5$ pretekárov. Každý pretekár prejde okruh vždy za rovnaký čas. Rozhodnite, či môžeme určiť:

• najrýchlejšieho pretekára počas šiestich kôl,
• druhého najrýchlejšieho pretekára počas siedmich kôl,
• tretieho najrýchlejšieho pretekára počas ôsmich kôl.

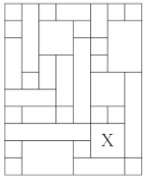
Na obrázku je mapa lesných ciest. Kôň Rafał je v ohraničenej časti lesa (označenej písmenom $X$). Koľkými rôznymi spôsobmi sa vie dostať Svorad z ľavého horného rohu lesa k Rafałovi, ak bude chodiť po cestách len smerom nadol alebo napravo? K Rafałovi sa dostane, ak bude na križovatke ciest susediacej s časťou lesa, kde je Rafał. Keď sa raz dostane k Rafałovi, zastane a ďalej už nejde.