Zadania seminára Malynar, 30. ročník - Zimný semester

1. séria - Zimný semester
2. séria - Zimný semester

Vzorové riešenia 1. série nájdeš v časopise Malynar-30-2

Vzorové riešenia 2. série nájdeš v časopise Malynar-30-3

Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.

Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.

Termín série: 19. október 2020 20:00:00

1. Artuš, Bambi, Celestia a Dolores sa hádajú o tom, kto z nich ich prihlásil na súťaž. Po otázke, kto to urobil, nám povedia toto:

Artuš: “Bambi poslala prihlášku. Ja som to nebol.”
Bambi: “Celestia ju poslala. Artuš to naozaj nebol.”
Celestia: “Bambi to nebola. Ja som poslala tú prihlášku.”
Dolores: “Celestia to nebola. Bol to Artuš.”

Vieme, že každý z nich povedal jednu pravdivú a jednu nepravdivú vetu. Vieme s určitosťou povedať, kto poslal prihlášku?

2. Medzi Artušom a Bambi prebehol tento rozhovor:

Bambi: "Koľko z tvojich súrodencov má práve $3$ sestry?"
Artuš: "Aspoň polovica z nich."
Bambi: "A koľko z tvojich súrodencov má aspoň $4$ bratov?"
Artuš: "Nie viac ako polovica z nich."

Koľko je možností na počty bratov a sestier, ktoré môže mať Artuš a aké to sú?

3. Číslo letu je trojciferné prirodzené číslo, ktoré má všetky svoje cifry nepárne. Ak k nemu pripočítam $421$, dostanem trojciferné číslo, ktoré má všetky svoje cifry párne. Nájdite všetky čísla letu, ktoré to spĺňajú.

4. Máme úsečku $AD$. Na nej vyznačíme body $B$ a $C$ tak, že $|AB| < |AC|$ a platí $|AC| = 2 \cdot |AB| + |CD|$. Vieme, že $CXB$ je pravouhlý trojuholník s pravým uhlom pri vrchole $C$ a $45^{\circ}$ veľkým vnútorným uhlom pri $X$. Jeho strana $CX$ je dlhá $14$ cm. Aká je dlhá pôvodná úsečka $AD$?

5. Mýtický boh Šari ukladá hory do políčok mriežky $3\times3$. Do každého políčka môže položiť ľubovoľný počet hôr a niektoré políčka môže nechať aj prázdne. Keď ich uloží, tak spočíta počet hôr v každom riadku aj v každom stĺpci. Snaží sa ich uložiť tak, aby týchto $6$ počtov bolo navzájom rôznych. Koľko najmenej hôr na to mýtický boh Šari potrebuje? Vysvetlite, prečo mu na to menej hôr nestačí a nakreslite, ako ich má uložiť.

6. Ujo mal kalkulačku, ktorá vybuchne, ak sa na nej zobrazí číslo menšie ako $0$. Na začiatku je na kalkulačke číslo $1$. Sú na nej iba tlačítka s operáciami $-6, -42$ a $*7$. Koľko čísel od $1$ do $1000$ (vrátane) vie pomocou týchto operácií na kalkulačke získať? Na kalkulačke sa počas výpočtu môžu zobraziť aj čísla väčšie ako $1000$.

Vzorové riešenia 1. série nájdeš v časopise Malynar-30-2

Vzorové riešenia 2. série nájdeš v časopise Malynar-30-3

Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.

Termín série: 23. november 2020 20:00:00

1. Dolores má presýpacie hodiny, ktoré sa celé presypú za $4$ minúty, a presýpacie hodiny, ktoré sa presypú za $11$ minút. Navrhnite postup, ako pomocou týchto dvoch presýpacích hodín odmerá $10$ minút.

2. Celestia si predstavovala päť kamarátov, ktorí sa dohadujú, kto spolu pôjde na dovolenku. Zistite, kto nakoniec šiel, ak viete, že platí:

Ak išla Uršula, tak išiel aj Zdeno. (To znamená, že Zdeno môže ísť, aj keď Uršula nepôjde.)
Išla buď Xilofénia, alebo Viktor, alebo obaja spolu.
Išiel buď Zdeno, alebo Yvon, ale nie obaja spolu.
Viktor a Yvon išli buď obaja spolu, alebo ani jeden.
Ak išla Xilofénia, tak išli aj Uršula a Viktor. (Každý z dvojice Uršula a Viktor môže ísť, aj keď Xilofénia nepôjde.)

3. Gazdiná Iréna pripravila $25$ sushi pre ľudí pri stole. Potom spočítala, že by si každý mohol zobrať dva, ale po troch by už na všetkých nevyšlo. Povedala si, že keby vyrobila ešte $10$ sushi, mohol by si každý pri stole vziať tri, ale štyri nie každý. Nakoniec prichystala dokopy $52$ sushi. Každý pri stole by si teda mohol vziať štyri sushi, ale po päť by už na všetkých nevyšlo. Koľko ľudí pri stole gazdiná Iréna čakala?

4. Do šachovnice $7\times7$ vpíšeme postupne čísla od $1$ do $49$ tak, že začneme v ľavom hornom rohu, a pokračujeme postupne po riadkoch. Vieme na túto šachovnicu položiť $3$ tetrominá ako na obrázku tak, aby súčet všetkých čísel prekrytých týmito tetrominami (tetrominá sa nemôžu prekrývať navzájom) bol deliteľný $4$? obrazok

5. Čierni nindžovia sa chystajú útočiť a starček predpovedal, za koľko minút by prišli. Predpovedal $5$ časov v minútach (minúty sú celé a hodnoty predpovedí sa môžu opakovať). Vypočítal súčty všetkých dvojíc medzi nimi. Vyšli mu však len tri rôzne výsledky: $57, 70$ a $83$. Aký bol najväčší počet minút, ktorý predpovedal?

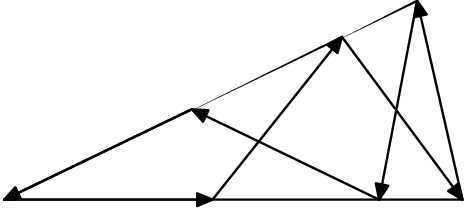
6. E skáče svojím prstom po dvoch ramenách uhla ako na obrázku. Všetky jeho skoky sú rovnakej dĺžky. Začína z vrcholu uhla a po siedmich skokoch sa vráti naspäť do tohto vrcholu. Aká je veľkosť tohto uhla? obrazok