Balónov bolo sedem a na každom z nich bolo napísané jedno číslo. Ak by sme sčítali čísla na všetkých siedmich balónoch, vyšlo by nám $280$. Súčet čísel na tých štyroch, ktoré im ostali, je $178$. Dievčatkám uleteli tri balóny: modrý, zelený a červený. Na zelenom bolo napísané číslo dvakrát väčšie ako na modrom. Na červenom balóne bolo číslo trikrát väčšie ako na modrom balóne. Aké čísla boli na balónoch, ktoré uleteli? Nájdite všetky riešenia a odôvodnite, že iné nie sú.

Perník má pred sebou dve drevené kocky a chcel by na ich steny napísať čísla od $0$ po $9$ tak, aby bolo pomocou nich možné vyskladať každé číslo od $01$ po $31$ (jednociferné čísla sú s nulou na začiatku, takže vždy je potrebné použiť obe kocky). Čísla na stenách kocky sa môžu samozrejme opakovať. Vie perník dané čísla takto rozdeliť? Ak áno, ako? Ak nie, prečo? Svoje riešenie poriadne zdôvodnite.

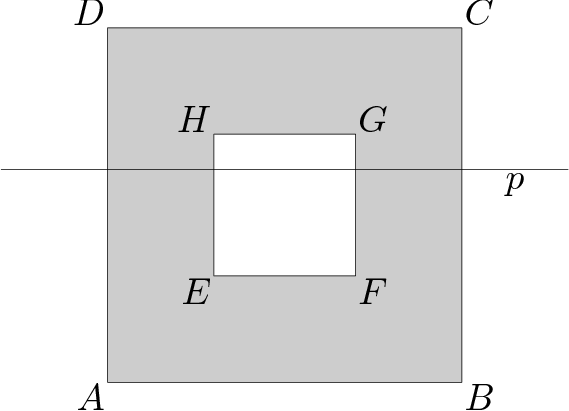
Na obrázku je štvorec $ABCD$ so stranou dĺžky 10 cm. Vnútri neho leží menší štvorec $EFGH$. Vieme, že strany $AB$, $CD$, $EF$ a $GH$ sú všetky navzájom rovnobežné a strana $EF$ je rovnako vzdialená od $AB$ ako strana $GH$ od $CD$. Strana $EH$ je rovnako vzdialená od $AD$ ako strana $FG$ od $BC$. Plocha vnútri $ABCD$ a zároveň mimo štvorca $EFGH$ je označená sivou. Priamka $p$, ktorá je rovnobežná s $AB$ vo vzdialenosti 6 cm, rozdeľuje sivú plochu na dve časti (ako na obrázku). Obsah jednej časti je o 12 cm ² väčší ako obsah druhej. Vypočítajte dĺžku strany $EF$. Úlohu neriešte rysovaním.

Počet myšiek je trojciferné prirodzené číslo. Súčet cifier počtu myšiek je $11$. Keď vezmeme jeho cifry a každú z nich vynásobíme samú so sebou a následne tieto súčiny sčítame, tak dostaneme $45$ (napr. ak máme číslo 142, tak dostaneme $1 \cdot 1 + 4 \cdot 4 + 2 \cdot 2 = 21$). Ak od tohto čísla odčítame $198$, získame trojciferné číslo, v ktorom sú tieto cifry v opačnom poradí. Aké je pôvodné číslo? Nájdite všetky možnosti a zdôvodnite, prečo iné nie sú.

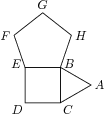
Stánok sa skladá z rovnostranného trojuholníka $ABC$, štvorca $BCDE$ a pravidelného päťuholníka $EFGHB$, ako vidno na obrázku. Aký je rozdiel medzi uhlami $ADE$ a $AHE$? Ak máte s úlohou problém, tak by vám mohlo pomôcť naše Edukačné okienko z minuloročného časopisu Malynár-28-4. Úlohu neriešte rysovaním.

a) Na súťaži je $8$ súťažiacich. Odohrali sa $3$ kolá zápasov, pričom v každom kole každý súťažiaci musel s niekým hrať. Nikto nehral viackrát s rovnakým súperom. Po konci celej súťaže si rozhodca povedal, že chce súťažiacich rozdeliť do dvoch skupín tak, aby každý súťažiaci hral iba so súťažiacimi zo svojej skupiny. Mohol turnaj prebehnúť tak, aby sa mu toto rozdelenie podarilo? Ak áno, ako? Ak nie, prečo?
b) Na súťaži máme $10$ tímov. Odohrali sa $4$ kolá zápasov, pričom v každom kole každý tím musel s niekým hrať. Nikto nehral viackrát s rovnakým súperom. Po konci celej súťaže si rozhodca povedal, že chce tímy rozdeliť do dvoch skupín tak, aby každý tím hral iba s tímami zo svojej skupiny. Mohol turnaj prebehnúť tak, aby sa mu toto rozdelenie podarilo? Ak áno, ako? Ak nie, prečo?

O lístok na atrakciu sa hádali jednorožec, Cukrová Lama a myška. Perníček povedal Cukrovej Lame: Lama, ty si nevyhrala. Ale dostaneš aspoň nejaké tokeny. Potom povedal jednorožcovi: Lama naozaj nevyhrala. A dokonca ani nedostane tokeny. Nakoniec povedal myške: Myška, nebola si najlepšia. Víťazom je jednorožec. Na záver ešte dodal, že každému povedal najviac jednu nepravdivú vetu. Kto vyhral lístok a prečo?

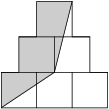
Keď sa na kôš pozeráme zhora, otvor vyzerá ako pyramída na obrázku, ktorá sa skladá zo $6$ rovnakých symetricky uložených štvorcov (vždy v stredoch v strán). Lístok sa nachádza niekde na vrchu v sivej časti. Akú plochu musí Perníček prehľadať, aby našiel lístok, ak celá pyramída má obsah $600$?

V trojpodlažnom dome (prvé podlažie je najspodnejšie a tretie najvrchnejšie), do ktorého perníček prišiel, sa momentálne nachádza $42$ stvorení, pod ktorými (na nižších podlažiach) sa niekto nachádza a $48$ stvorení, nad ktorými (na vyšších podlažiach) sa niekto nachádza. Na druhom podlaží je momentálne polovica všetkých stvorení nachádzajúcich sa v dome. Koľko je všetkých stvorení v dome? Koľko stvorení sa nachádza na každom podlaží?

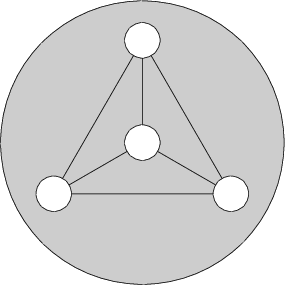
Na obrázku sú vyznačené 4 bodky a 4 sivé oblasti. Do každej bodky a každej oblasti chceme napísať jedno prirodzené číslo od 1 do 8 (každé číslo môžeme použiť práve raz). Navyše musí platiť, že číslo, ktoré je napísané v každej oblasti je vždy tretinou súčtu troch čísel, ktoré sú v bodkách, ktoré sa dotýkajú, respektíve nachádzajú v danej oblasti. Vieme takto čísla rozdeliť? Svoje riešenie zdôvodnite.

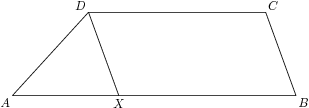
Posteľ má tvar lichobežníka $ABCD$ s dĺžkami základní $|AB|=8$ a $|CD| = 5$. Lichobežník je taký štvoruholník, ktorého dve strany (základne) sú navzájom rovnobežné. Uhol $BCD$ má $110$ stupňov a uhol $BAD$ má $50$ stupňov. Bod $X$ leží na strane $AB$ tak, že $|AX| = 3$. Perníček si bude vedieť správne naštelovať posteľ, keď zistí veľkosť uhla $ADX$. Ak máte s úlohou problém, tak by vám mohlo pomôcť naše Edukačné okienko z minuloročného časopisu Malynár-28-4. Úlohu neriešte rysovaním.

Na tabuľke máme číslo $1$. Vždy môžeme vykonať jednu z týchto akcií:

• ku číslu pripočítať $9$
• ak je číslo aspoň $6$, tak od neho odpočítať $6$
• vynásobiť ho samým sebou