Štyria mušketieri Aramis, Bathos, Corthos a D'Artagnan stoja na štvorcovom námestí vydláždenom ako na obrázku. Každý z nich stojí sám na jednej dlaždici. Povedali nasledovné výroky:

• Aramis: „Stojím na dlaždici s rovnakým znakom ako Bathos, ale s Bathosom nesusedím ani stranou, ani rohom“.
• Bathos: „Nestojím v rohu. Aramisova dlaždica susedí stranou alebo rohom s dlaždicami všetkých znakov okrem toho, na ktorom stojí.“
• Corthos: „Stojím na dlaždici so štvorcom.“
• D'Artagnan: „Stojím na dlaždici s iným znakom ako Corthos a moja dlaždica susedí s Corthosovou dlaždicou stranou.“

Cez rieku bola vytvorená cestička z kameňov v tvare štvorcov a kruhov, ako na obrázku. Tabuľka pri brehu mu povedala, že na to, aby cez rieku prešiel, musí do kamienkov zapísať čísla $1$, $2$, $4$, $5$, $6$, $9$, $10$, $11$ a $13$, každé práve raz. Číslo v každom kruhovom kamienku sa rovná súčtu čísel v jeho dvoch susedných štvorcových kamienkoch. Aký je najväčší možný súčet čísel v dvoch štvorcových kamienkoch na kraji? Vysvetlite, prečo sa väčší súčet nedá dosiahnuť.

Čiapočka a Vlk majú každý svoj košík o kapacite štyroch klobás. Vkladajú do ľubovoľného z nich klobásy očíslované číslami $1$ až $8$, každú práve raz, až kým nebudú oba zaplnené. Čiapočka začína a v ťahoch sa striedajú, pričom Čiapočka vyhrá, ak bude väčší súčin čísel klobás v jej košíku. Vlk vyhrá, ak bude väčší súčin čísel klobás v jeho košíku. Pre ktorého z hráčov existuje výherná stratégia, a aká? Výherná stratégia je postup, podľa ktorého ak hráč hrá, tak vyhrá bez ohľadu na ťahy súpera.

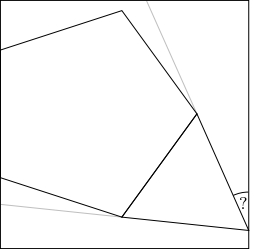
Domček spadol a vyvrátil sa na bok. Vnútri štvorca sa nachádza pravidelný päťuholník, ktorý zdieľa stranu s rovnostranným trojuholníkom ako na obrázku. Vypočítajte veľkosť vyznačeného uhla.

Kráľ Drozdia brada a Pyšná princezná majú v záhrade na stole $10$ dukátov s číslami od $1$ po $10$, každý z nich je buď strieborný alebo zlatý. Dukát s číslom $5$ je zlatý a aspoň jeden iný dukát je strieborný. Ak sú dva dukáty vyrobené z rôznych kovov, tak potom bude platiť, že dukát s ich súčtom je strieborný a s ich súčinom je zlatý. Akej farby sú jednotlivé dukáty? Nájdite všetky možnosti a ukážte, že žiadne iné neexistujú.

V kruhu stál párny počet bratov. Jednému z nich sa magicky vo vrecku zjavila zlatá minca. Polovica z bratov nato povedala: „Mincu mám vo vrecku ja alebo jeden z mojich susedov.“ Druhá polovica bratov povedala: „Mincu nemám vo vrecku ani ja, ani žiaden z mojich susedov.“ Koľko mohlo byť dokopy bratov, ak práve dvaja z nich klamali? Nájdite všetky možnosti a ukážte, že žiadne iné neexistujú.

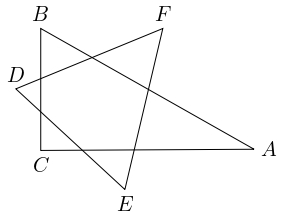
Hviezda mala tvar dvoch prekrývajúcich sa trojuholníkov ako na obrázku. V trojuholníku \(ABC\) má uhol \(CAB\) veľkosť $30°$ a uhol \(ACB\) veľkosť $90°$. Strany trojuholníka \(DEF\) vytvorili tri trojuholníky vnútri trojuholníka \(ABC\). Tieto trojuholníky sú rovnoramenné, pričom ich základne sú časti strán trojuholníka \(DEF\) vnútri trojuholníka \(ABC\), a ich vrcholy oproti základniam sú vrcholy \(A\), \(B\) a \(C\). Aké sú veľkosti uhlov v trojuholníku \(DEF\)?

Rybička povedala Ozzymu svoju úlohu. Päťciferné číslo \(\overline{PQRST}\) sa skladá z cifier $1$, $2$, $3$, $4$, $5$. Trojciferné číslo \(\overline{PQR}\) je násobkom čísla $4$, \(\overline{QRS}\) násobkom čísla $5$, \(\overline{RST}\) je násobkom čísla $3$. Nájdite všetky možnosti aké môže byť číslo \(\overline{PQRST}\) a ukážte, že žiadna iná možnosť neexistuje.

Mapa mala tvar obdĺžnikového papiera a na nej boli nakreslené $4$ cesty ako $4$ čiary \(A, B, C\) a \(D\), ktoré sú rovnobežné so stranou obdĺžnika tak, ako na obrázku. Vieme, že platí:

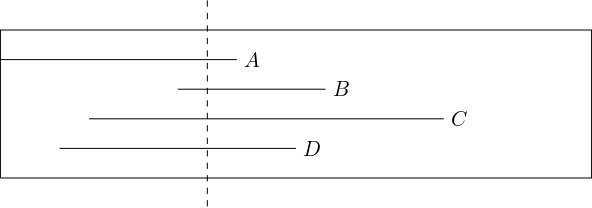
• Čiara \(A\) má dĺžku \(\SI{8}{cm}\) a jej ľavý okraj sa dotýka ľavého okraju papiera.
• Čiara \(B\) má dĺžku \(\SI{6}{cm}\) a jej ľavý okraj je od ľavého okraja papiera vzdialený \(\SI{6}{cm}\).
• Čiara \(C\) má dĺžku \(\SI{12}{cm}\) a jej ľavý okraj je od ľavého okraja papiera vzdialený \(\SI{3}{cm}\).
• Čiara \(D\) má dĺžku \(\SI{8}{cm}\) a jej ľavý okraj je od ľavého okraja papiera vzdialený \(\SI{2}{cm}\).

Mama koza odišla na nákupy a ostatných šesť kozliatok išlo do školy. Týchto šesť kozliatok sa potom postupne vracia zo školy domov v nejakom poradí. Vieme o nich toto:

• Žiadne dve kozliatka neprišli naraz.
• Barbora môže byť doma spolu s Andrejom len vtedy, keď je tam s nimi aj Claudia.
• Dušan prišiel domov pred Ferkom.
• Edo prišiel domov až po Andrejovi.
• Edo môže byť doma spolu s Andrejom len vtedy, keď je tam s nimi aj Ferko.
• Claudia neprišla prvá a ani posledná.
• Dušan prišiel domov až po Barbore.
• Keď prišiel Dušan domov, tak tam boli už aspoň traja jeho súrodenci.

Pritom ako postavili vojačikov do radu, tak sa na zem vedľa seba otlačilo niekoľko celých čísel. Súčet každých $7$ vedľa seba napísaných čísel je párne číslo. Súčet každých $8$ vedľa seba napísaných čísel je nepárne číslo. Koľko najviac čísel môže byť takto napísaných?

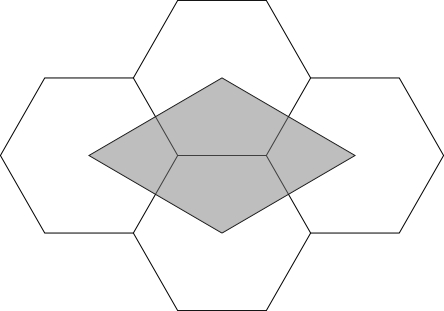
Portál je zložený zo štyroch zhodných pravidelných šesťuholníkov, ktoré sa dotýkajú ako na obrázku. Pri portáli stála tabuľka s finálnou otázkou. Koľkokrát väčší je obsah sivého štvoruholníka tvoreného ich stredmi ako obsah jedného šesťuholníka?