V piesku je nakreslená cesta tvaru priamky, na ktorej sú nejak umiestnené štyri body predstavujúce mestá $A, B, C, D$ (nie nutne v tomto poradí) pričom $|AD|=1$, $|BC|=2$, $|BD|=3$, $|AB|=4$ a $|CD|=5$. Zistite vzdialenosť miest $A$ a $C$.

Na mape je 5 miest. Je možné tieto mestá spojiť cestami tak, aby z každého mesta vychádzali práve 3 cesty, pričom cesty sa navzájom nemôžu pretínať a platí, že z každého mesta sa nejakou trasou vieme dostať do každého iného? Dvojica miest môže byť prepojená nanajvýš jednou cestou a mesto nemôže byť spojené so samým sebou. Ak áno, ukážte ako, ak nie, vysvetlite prečo. A čo keby bolo miest 8?

O Prvom, Druhom a Treťom vieme, že každý z nich má iný počet rokov. Zároveň nám o nich bolo povedané:

• Druhý je starší ako Tretí.
• Tretí je starší ako Prvý.
• Prvý je starší ako Druhý.
• Súčet vekov Prvého a Tretieho je dvojnásobkom veku Druhého.

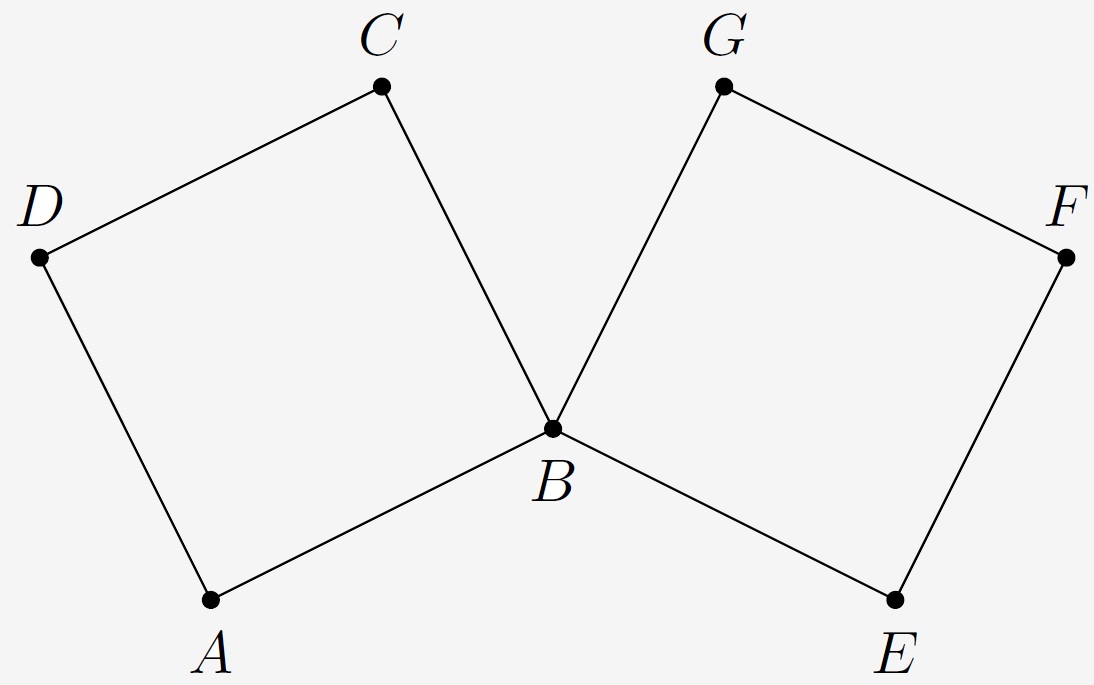
V tme vyzeral pôdorys stanov ako dva štvorce $ABCD$ a $BEFG$ ako na obrázku tak, že $|AB| = |BE|$ a uhol $CBG$ má $60°$. Zistite veľkosť uhla $CFG$.

Majme tabuľku $6×6$. Postava a Duke na nej hrajú hru. Striedavo na ňu umiestňujú dominá (dieliky s rozmermi $1×2$). Hráč prehráva vtedy, keď už do tabuľky nevie umiestniť domino. Kto z hráčov má víťaznú stratégiu a prečo? Čo ak by sme mali tabuľku $7×7$ a hráči by na ňu umiestňovali triminá s rozmermi $1×3$? Víťazná stratégia je postup, podľa ktorého, keď jeden hráč hrá, tak vyhrá bez ohľadu na ťahy súpera.

Heslo je 6-ciferné číslo, ktoré neobsahuje cifru 0 ani 1. Keď vezmeme všetky 2-ciferné podčíslia, ktoré sa v ňom nachádzajú (napr. pre číslo 123456 to sú 12, 23, 34, 45 a 56), tak sú všetky rôzne a platí pre ne:

• Práve jedno z nich je deliteľné číslom 6.
• Práve dve z nich sú deliteľné číslom 3.
• Práve dve z nich sú prvočísla (prvočísla sú také čísla, ktoré majú práve dvoch deliteľov - 1 a samé seba).
• Práve tri z nich majú obe cifry rovnaké.

Máme tri príšery. Príšery s párnym počtom nôh vždy hovoria pravdu a príšery s nepárnym počtom nôh vždy klamú. Zazneli výroky:

• Argo: Bret má 6 nôh. Ja a Bret máme spolu párny počet nôh.
• Bret: Ja mám 8 nôh. Chuck má 4 nohy.
• Chuck: Bret a Argo majú spolu 15 nôh.

Uzamknutie sa vypína zasunutím kombinácie kartičiek do terminálu. Máme kartičky s číslami od 1 do 8. Chceme nájsť štyri rôzne rozdelenia kartičiek do dvoch skupín tak, aby v oboch skupinách bol rovnaký súčet čísel na kartičkách a zároveň, aby počet kartičiek v skupinách bol rôzny (platí, že rozdelenie, kde by sme mali v prvej skupine kartičky $1,2,3$ a v druhej $4,5,6,7,8$, je to isté, ako keby sme mali v prvej skupine $4,5,6,7,8$ a v druhej $1,2,3$). Podarí sa nám to? Ak áno, ako? Ak nie, prečo?

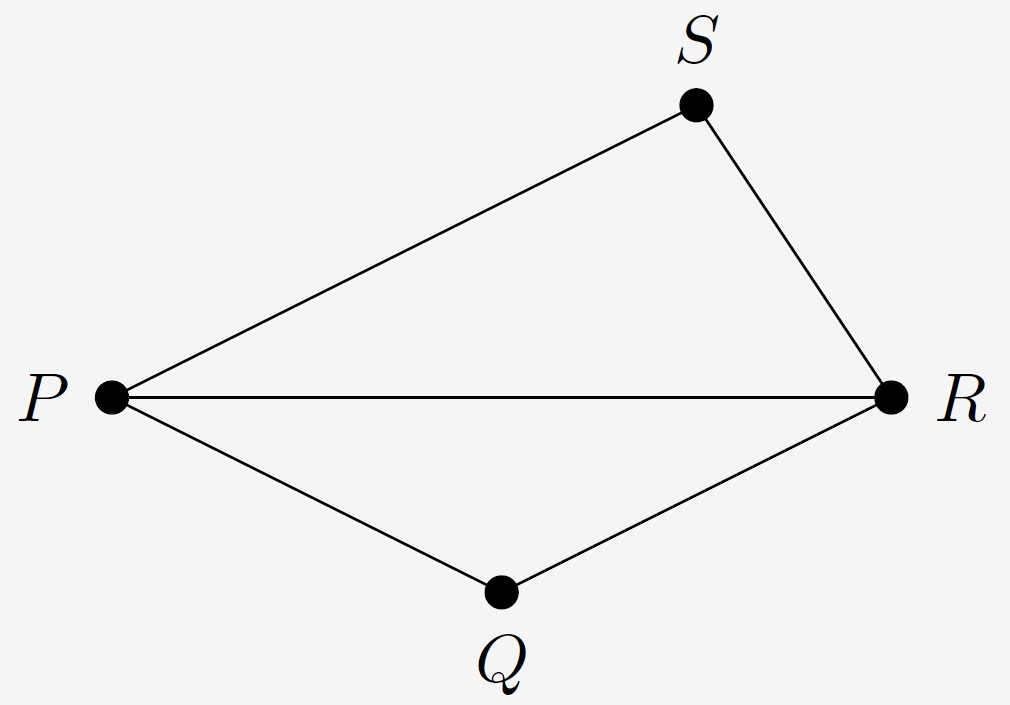
Kľučka má body $P$, $Q$, $R$, $S$ ako na obrázku. Platí, že $|PQ| = |QR|$, uhol $PSR$ má 110 stupňov, úsečka $PR$ delí uhol $SPQ$ na dve rovnaké časti a uhol $SPR$ je štyrikrát menší ako uhol $PRS$. Aká je veľkosť uhla $PQR$?

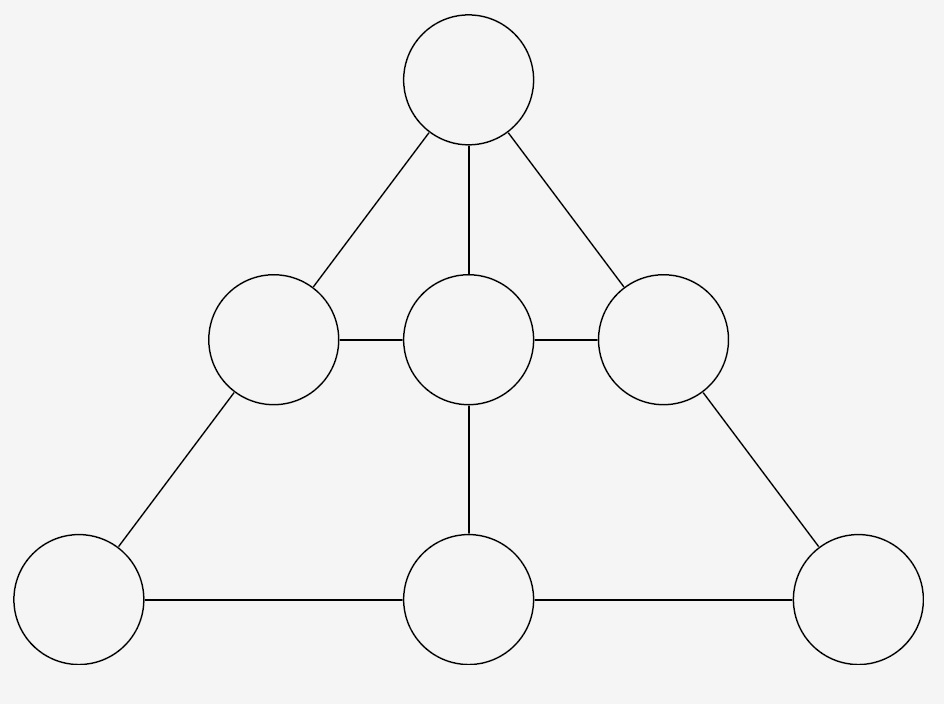
Terminál na obrazovke mal tvar pyramídy ako na obrázku. Greg chce napísať čísla od 1 do 7 do krúžkov na obrázku (každé práve raz), tak, aby platilo, že súčet každých troch čísel na úsečke je rovnaký pre každú trojicu. Ktoré čísla môžu byť v hornom krúžku pri takomto vyplnení? Pre každé takéto číslo uveďte príklad vyplnenia. Vysvetlite, prečo ostatné čísla nemôžu byť v hornom krúžku.

Sam za sebou vždy ťahá čiaru a hýbe sa nasledovne: Povieme mu číslo a on ho vydelí štvorkou tak, že dostane celočíselný podiel a zvyšok. Ak mu ostane zvyšok 1, pohne sa o meter na sever, ak 2, tak na juh, ak 3, tak na východ a ak 0, tak na západ. Následne postup zopakuje s celočíselným podielom, ktorý mu ostal. Tento proces opakuje až kým raz nedostane podiel 0 (vtedy urobí posledný pohyb). Aké je najmenšie číslo také, že ak ho povieme Samovi, tak nakreslí svojou trasou štvorec so stranou 1 meter? Prečo to pre žiadne menšie nefunguje?

Na úsečke $AB$ so stredom $S$ vyrástlo 100 dvojíc tulipánov tak, že pre každú dvojicu leží bod $S$ uprostred. Platí, že 100 tulipánov vykvitlo na červeno a 100 na žlto. Dokážte, že súčet vzdialeností žltých tulipánov od bodu A je rovnaký ako súčet vzdialeností červených tulipánov od bodu B.