Malynár

Pozrite sa na

Pravidlá Príspevky Úlohy Výsledky Časopisy Fotografie Kalendár Newsletter Online sústredenia Mamut Máš problém?! 2 % pre STROM TMM Minisústredenia Denný tábor Šifrovačka Kôš Kontakty Ochrana osobných údajov

Správa účtu

Prihlásiť sa Zaregistrovať sa

Zadania seminára Malynar, 29. ročník - Zimný semester


Vzorové riešenia 1. série nájdeš v časopise Malynar-29-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-29-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 21. október 2019 20:00:00
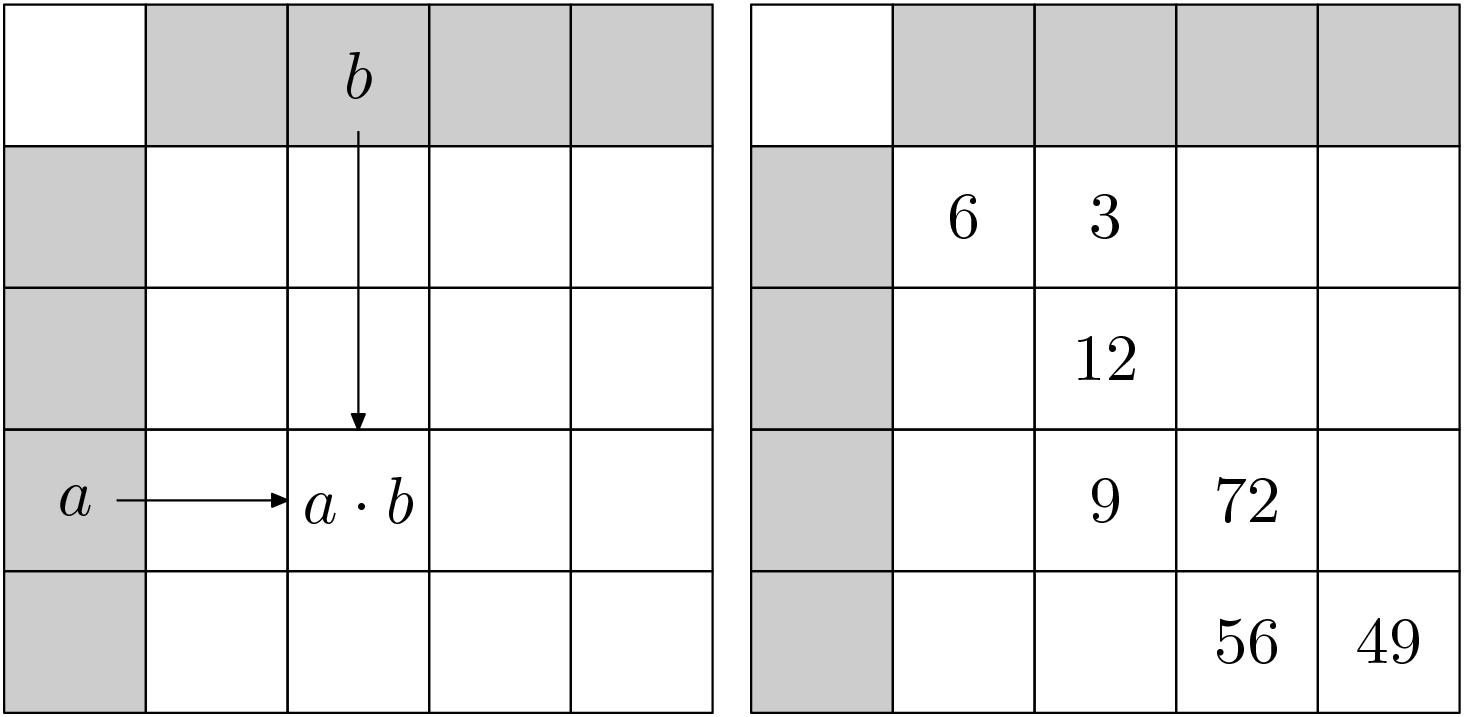
1. Na zámku bola tabuľka $5\times 5$. Časť tabuľky bola už vopred vyplnená (obr. $2$). Tárajko musí doplniť tabuľku tak, aby v každom bielom políčku bol súčin príslušných čísel z dvoch sivých záhlaví v riadku a stĺpci (ako na obr. $1$). V sivých políčkach môžu byť iba prirodzené čísla. Pomôžte Tárajkovi nájsť všetky možné riešenia a zdôvodnite, že to inak nejde.

malynar29-1-1-1
2. Tárajko vedel, že sitko je drahé, a teda jeho cena je dvojciferné číslo. Opýtal sa na ňu štyroch predavačov a tí mu povedali toto:
  • Adam: ,,Jedna z cifier je dvakrát väčšia ako druhá.‘‘
  • Branči: ,,Cena je deliteľná šiestimi.‘‘
  • Cyril: ,,Keby sme k cene prirátali $3$, bola by deliteľná piatimi.‘‘
  • Drahoslav: ,,Cena je menšia ako $20$.‘‘
Tárajko vie, že práve jeden z nich klame. Určte správnu cenu a dokážte, že je jediná správna.
3. Starček priniesol tabuľku s napísanými číslami $1$, $2$, $3$, $\dotsc$, $100$. V každom kole zmazal dve z čísel a napísal namiesto nich ich súčet. Po čase v tabuľke ostalo päť po sebe idúcich čísel. Ktoré to boli? Svoje riešenie zdôvodnite.
4. Predavač mal štyri čajové vrecúška s viacerými druhmi čajov. V najľahšom je mätový čaj, v najťažšom je harmančekový čaj a zvyšné dve vrecúška majú rovnakú hmotnosť. Má aj rovnoramenné váhy, na ktorých vie vážiť vrecúška. Vrecúška sa vážia tak, že na každé rameno sa dá práve jedno vrecúško a porovná sa ich váha. Na koľko najmenej vážení vie s určitosťou zistiť, kde je mätový a kde je harmančekový čaj, ak pri každom vážení musí byť na každom ramene váhy práve jedno čajové vrecúško? Zdôvodnite, prečo to na menej vážení nejde, a napíšte, ako ste postupovali.
5. Pred zámkom boli tri jazierka. Do prvého sa zmestí $96$ žubrienok, do druhého $104$ a do tretieho $144$. Každú noc sa v jazierku rozdelí každá žubrienka na dve. Ak je žubrienok veľa a nemôžu sa rozdeliť všetky, nerozdelí sa ani jedna. Tárajko má k dispozícii práve tri žubrienky na každé jazierko. Každú žubrienku môže ráno nasadiť do jazierka v deň, ktorý si zvolí. Žubrienky Tárajko nemôže z jazierok nikdy vyberať. Ako ich má postupne nasádzať do jazierok tak, aby boli čo najskôr všetky tri jazierka úplne zaplnené? Ktorý deň v poradí sa to stane? Prečo to nejde za menej dní?
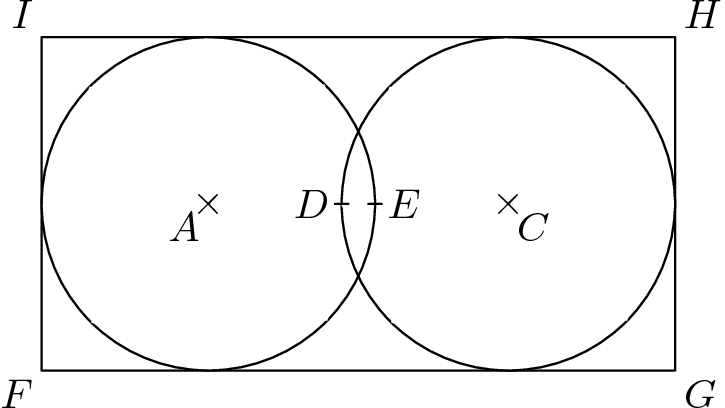
6. Na gobelíne sú nakreslené dve rovnako veľké pretínajúce sa kružnice a okolo nich obdĺžnik $FGHI$ tak, že kružnice obdĺžnik nepretínajú, no každá má s ním tri spoločné body (ako na obrázku). Boli tam tiež vyznačené niektoré zaujímavé body -- stredy kružníc ako body $A$ a $C$ a priesečníky úsečky $AC$ s kružnicami ako body $D$ a $E$. Aký je súčet obsahov trojuholníkov $FDI$ a $FGE$, ak polomer kružnice je $10$ $cm$ a obsah obdĺžnika je $760$ $cm$2? Úlohu neriešte rysovaním.

malynar29-1-1-6

Vzorové riešenia 1. série nájdeš v časopise Malynar-29-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-29-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 25. november 2019 20:00:00
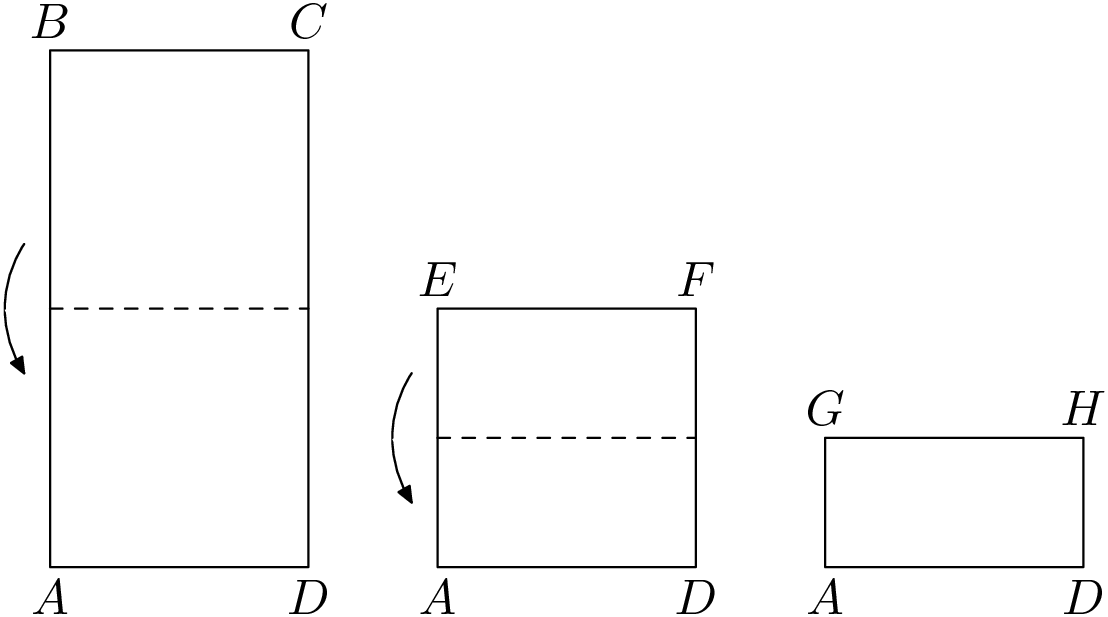
1. Tárajka zaujal obrúsok. Mal tvar obdĺžnika $ABCD$. Ak ho preložíme na polovicu, dostaneme obrúsok v tvare obdĺžnika $ADFE$. Ak to isté spravíme s obdĺžnikom $ADFE$, získame obdĺžnik $ADHG$ (ako na obrázku). Obvod obdĺžnika $ADHG$ je $24$ $cm$ a obdĺžnika $ABCD$ $48$ $cm$. Aký je obsah obdĺžnika $ABCD$? Úlohu neriešte rysovaním.

malynar29-1-2-1
2. V jazierku plávalo $10$ žubrienok v kruhu. Na chrbtoch mali nejako rozmiestnené všetky čísla od $1$ do $10$. Žubrienky s číslami $1$, $3$, $5$, $7$ a $9$ sú na nepárnych pozíciách v kruhu a žubrienky s číslami $2$, $4$, $6$, $8$ a $10$ sú na párnych. Tárajko na nich poriadne nedočiahol, takže mohol urobiť iba nasledovné:
  • K číslu vybranej žubrienky pripočítať súčet jej susedov.
  • Od čísla vybranej žubrienky odčítať rozdiel čísel žubrienok vzdialených $2$.
Môže Tárajko dosiahnuť rovnosť súčtov čísel na chrbtoch žubrienok na nepárnych a párnych pozíciách? Svoju odpoveď zdôvodnite.
3. Cestou do krčmy rátal domy. Vyšlo mu päťciferné číslo. Toto číslo neobsahuje cifry $0$ ani $1$, ale určite obsahuje práve jednu cifru $6$. Je v ňom párny počet párnych číslic. Druhá až štvrtá číslica sú menšie ako $4$ a v čísle vieme dvakrát nájsť dve susediace číslice, ktoré sa rovnajú. Štvrtá cifra udáva, koľko je v čísle dvojok. Okolo koľkých domov prešiel Tárajko? Nájdite všetky možnosti a odôvodnite, že iné nie sú.
4. Štadión má tvar obdĺžnika $ABCD$ s dlhšou stranou $AB$. Uhlopriečky $AC$ a $BD$ zvierajú uhol $60^\circ $ (ten oproti kratšej strane štadióna). Futbalisti trénujú na veľkom okruhu $ACBDA$ alebo na malej dráhe $ADA$. Roland behal $10$-krát po veľkom okruhu a Benedikt $15$-krát po malej dráhe (to znamená, že po hrane $AD$ prebehol $30$-krát). Obaja dokopy ubehli $4,5$ km. Aká dlhá je uhlopriečka $AC$? Úlohu neriešte rysovaním! (Ak máte s úlohou problém, tak by vám mohlo pomôcť naše ,,Edukačné okienko‘‘ z minuloročného časopisu Malynár-28-4, ktorý nájdete na našej stránke.)
5. Sto šálkov si myslí celé číslo (všetci to isté). Každý buď stále klame, alebo stále hovorí pravdu. Najprv v nejakom poradí povedia vety: ,,Číslo je aspoň $1$.‘‘ ,,Číslo je aspoň $2$.‘‘ $\dotsc$ ,,Číslo je aspoň $100$.‘‘ Potom povedia v nejakom poradí vety: ,,Číslo je menšie ako $1$.‘‘ ,,Číslo je menšie ako $2$.‘‘ $\dotsc$ ,,Číslo je menšie ako $100$.‘‘ Koľko šálkov klame? Nájdite všetky riešenia a svoje riešenie odôvodnite.
6. Pole je veľké $7\times 7$ štvorčekov a na ňom niekde náhodne stojí armáda v podobe obdĺžnika s dĺžkami strán $3$ a $2$. Koľko najmenej striel musia šálkovia vystreliť z parného dela, aby si boli istí, že armádu zasiahli? Ukážte nejaký prípad rozmiestnenia striel a dokážte, že na menej to nejde.

Newsletter

Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!