Hubert našiel v lavici zabudnutú kocku, ktorá má na stenách ľubovoľne napísané čísla od $1$ po $6$, každé práve raz. Traja kamaráti sa zapozerali na kocku a všimli si, že každý ju vidí z inej strany a že každý vidí vrchnú stenu a dve susedné bočné steny. Zároveň platí, že každý z trojice vidí inú dvojicu bočných stien. Tiež si všimli, že ak sčítajú čísla, ktoré na stenách vidia, tak dostanú čísla $9, 14$ a $15$. Aké číslo môže byť na spodnej stene? Nájdite všetky možnosti a ukážte, že žiadne iné neexistujú.

Vo vílom údolí majú iba $3$ typy mincí s hodnotami $2, 5$ a tretiu hodnotu, ktorú Vanda práve zabudla. Vieme ale, že Hubert prvú zmrzlinu, ktorá stála $13$, nevedel zaplatiť menej ako troma mincami, ale troma mincami ju zaplatiť už vedel. Takisto druhú zmrzlinu za $19$ nevedel zaplatiť menej ako tromi mincami, no presne troma už áno. Aká je hodnota tretieho typu mincí? Nájdite všetky možnosti a ukážte, že žiadne iné neexistujú.

Hubert nalieval každé ráno hmlu do rozmanitých, rôzne veľkých nádob, ktoré si starostlivo zoradil na polici. Pri nalievaní postupoval postupne z jednej strany a žiadnu nádobu nepreskakoval. Do každej nádoby sa vojde aspoň liter hmly. Keby nalieval hmlu sedemdesiatlitrovou odmerkou, hmla z prvého nabratia by naplnila presne $11$ nádob, hmla z druhého nabratia by naplnila presne ďalších $12$ nádob a hmla z tretieho nabratia by naplnila presne ďalších $7$ nádob. Ak by použil päťdesiatlitrovú odmerku, tak hmla z prvého nabratia by naplnila presne $8$ nádob, z druhého nabratia presne ďalších $10$ nádob, z tretieho presne ďalších $7$ nádob a zo štvrtého presne ďalšie $4$ nádoby. Rozhodnite, či je tridsiata nádoba v poradí väčšia ako dvadsiata piata a poriadne zdôvodnite, prečo to tak musí byť.

Mapa knižnice je štvorčeková sieť $4 \times 4$, kde každý zo $16$ štvorčekov je zafarbený práve jednou zo $4$ farieb podľa toho, o akých vílach daná sekcia je: červená, modrá, zelená, žltá. Hubert vidí, že na mape je 9 rôznych $2 \times 2$ štvorcov.

1. Môže mapa vyzerať tak, že každý $2 \times 2$ štvorec obsahuje práve jeden štvorček z každej farby? Ak áno, nakreslite ako, ak nie, vysvetlite prečo.
2. Môže mapa vyzerať tak, že každý $2 \times 2$ štvorec obsahuje práve jeden štvorček z každej farby a zároveň aspoň $2$ rohové štvorčeky veľkého $4 \times 4$ štvorca majú rovnakú farbu? Ak áno, nakreslite ako, ak nie, vysvetlite prečo.

Zvýraznená časť zadania sa zmenila 19.12.2023
Prišli do klubovne a Viktor Hubertovi vysvetlil, že každá víla celý čas buď klame alebo hovorí pravdu. Veterné víly sa vyjadrili takto:

• Anemoi: Kód obsahuje cifru $8$.
• Boreas: Kód obsahuje cifru $2$. Dogoda klame.
• Caelus: Kód je číslo deliteľné $3$. Kód je číslo menšie ako $90$.
• Dogoda: Kód je číslo deliteľné $7$. Klamú aspoň dvaja z nás.
• Eurus: Anemoi aj Caelus zároveň hovoria pravdu. Kód obsahuje cifru $9$. Kód má aspoň $3$ cifry.

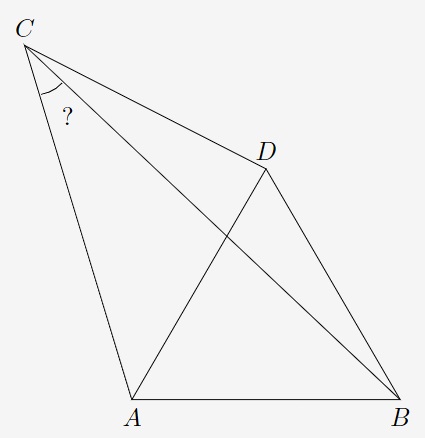
Strážca ukáže na niečo pripomínajuce portál v tvare trojuholníka. Označme si ho $ABC$. Vnútorný uhol trojuholníka $ABC$ pri vrchole A je väčší ako $60°$ a vnútorný uhol pri vrchole $B$ je menší ako $60°$. Ďalej je bod $D$ taký, že trojuholník $ABD$ je rovnostranný. Platí, že trojuholníky $ACD$ a $BCD$ sú rovnoramenné a to tak, že bod $D$ je oproti ich základniam. Určte veľkosť uhla $ACB$.

Nakoniec si vyžobronili dokopy $3$ informácie, z ktorých musia poskladať kód pre druhého strážcu. Zistili, že kód je štvorciferné číslo, ktoré musí spĺňať tieto podmienky:

1. Súčet číslic na mieste tisícok a mieste stoviek je rovný číslu, ktoré vznikne, ak z hľadaného čísla odstránime obe prostredné číslice.
2. Súčet z prvej podmienky je menší než dvojnásobok číslice na mieste desiatok.
3. Práve jedna zo štyroch číslic hľadaného čísla je prvočíslo (prvočíslo je číslo, ktoré má práve dvoch rôznych deliteľov, a to $1$ a seba samého).

Oblačník Cassius je štvorec $ABCD$ so stranou dlhou $6$ $cm$. Body $E$, $F$ a $G$ ležia postupne na stranách $AB$, $BC$ a $CD$, pričom platí, že $2 \cdot |EA| = |EB|$, $2 \cdot |F B| = |F C|$ a $2 \cdot |GC| = |GD|$. Cassius nadobudol tvar trojuholníka $EFG$. Určte obsah tohto trojuholníka.

Stretli 31 dedinčanov a medzi nimi si všimli $3$ skupiny - pravdovravci, klamári a premenliví. Pravdovravci vždy hovoria pravdu, klamári vždy klamú a premenliví si v prvej odpovedi vyberú, či hovoria pravdu alebo klamú a odvtedy to robia na striedačku. Chlapci sa najprv ale museli uistiť, kto je pravdovravec, klamár a premenlivý, takže sa ich všetkých spýtali $3$ otázky v tomto poradí: Na otázku „Si pravdovravec?“ dostali $22$ odpovedí áno. Na otázku „Si premenlivý?“ dostali $15$ odpovedí áno a na otázku „Si klamár?“ dostali $7$ odpovedí áno. Koľko je pravdovravcov, koľko klamárov a koľko premenlivých v Evalininej dedine?

Na stole je $20$ drahokamov. Dvaja hráči hrajú hru a striedajú sa v ťahoch. Hráč vo svojom ťahu musí zobrať aspoň $1$ a zároveň menej ako polovicu zo zostávajúcich drahokamov. Hráč, ktorý nemôže urobiť ťah podľa pravidiel, prehral. Pre ktorého z hráčov existuje výherná stratégia a aká? Výherná stratégia je postup, podľa ktorého, keď jeden hráč hrá, tak vyhrá bez ohľadu na ťahy súpera.

Máš $5$ kladných celých čísel. Keď ich sčítaš po dvoch všetkými možnými spôsobmi, vytvoríš $10$ čísel. Kráľovná mala nájsť také čísla, pre ktoré by tých $10$ čísel bolo po sebe idúcich. Hubert to skúšal, no nešlo to. Dokáž, že týchto $10$ čísel nemôže byť $10$ po sebe idúcich čísel.

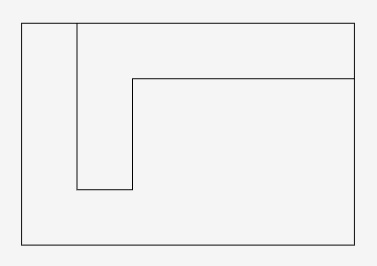
Drahokam v tvare obdĺžnika je rozdelený na osemuholník a šesťuholník ako na obrázku (pozor, obrázok je iba názorný, jednotlivé dĺžky nezodpovedajú skutočnosti). Strany osemuholníka majú veľkosti $1, 2, 3, 4, 5, 6, 7$ a $8$ v nejakom poradí. Nájdite maximálny možný obsah šesťuholníka za týchto podmienok.