
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Malynar, 33. ročník - Zimný semester
Vzorové riešenia 1. série nájdeš v časopise Malynar-33-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-33-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 23. október 2023 20:00:00
1. Na lúke rastú tri druhy rastlín, z každého druhu je tam aspoň jedna. Modré rastliny majú vždy jeden kvet a dva listy. Žlté rastliny majú vždy dva kvety a jeden list. No a napokon červené rastliny majú tri kvety a tri listy. Robin napočítal spolu na lúke $24$ kvetov a $24$ listov. Jeho kamarát John ale napočítal $25$ kvetov a $25$ listov. Jeden z nich počítal správne. Kto to bol a prečo? Vysvetlite, prečo ten druhý nemohol mať pravdu.
2. Piati kamaráti Anica, Ellie, Robin, John a Zara sa rozprávali. Vieme, že chodia do dvoch tried (z každej triedy je aspoň jedno dieťa), teda sú to dve skupiny spolužiakov. Žiaci z jednej triedy vždy buď všetci klamú, alebo všetci hovoria pravdu. Povedali tieto výroky:
- Anica: Som v triede sama.
- Ellie: John klame. Robin je môj spolužiak.
- Robin: Zara je moja spolužiačka.
- John: Anica nie je moja spolužiačka.
- Zara: Obe triedy majú aspoň dvoch žiakov.
3. Na mape boli zaznačené $4$ mestá Aris, Blei, Caun a Dlin. Mestá Aris, Blei a Dlin ležia na jednej priamke, pričom mesto Dlin leží medzi mestami Aris a Blei. Mesto Caun na tejto priamke neleží. Vzdialenosť miest Aris a Caun je rovnaká ako vzdialenosť miest Caun a Dlin a miest Dlin a Blei. Uhol medzi cestami, ktoré vedú z mesta Caun do miest Dlin a Blei je $30$ stupňov. Ellie sa rozhodla všetko lepšie preskúmať, a tak sa vydala po ceste z mesta Caun do mesta Dlin, ale miesto toho, aby zastala v meste Dlin, pokračovala rovnakým smerom a prešla ešte raz toľko. Presne na mieste, kde zastala, našla studňu. Dokážte, že cesta spájajúca studňu s mestom Aris je rovnobežná s cestou spájajúcou mestá Blei a Caun. Všetky cesty na mape sú znázornené úsečkami.
4. Väzenie má tvar šachovnice s rozmermi $5 \times 5$ a na nej jedno políčko ako vchod a jedno ako východ.
Aby sa deti dostali von, musia prebehnúť cez šachovnicu, pričom vstúpia vchodom a chcú z nej vyjsť východom. Vždy sa vedia pohnúť len na jedno z políčok, ktoré s tým, na ktorom stoja, susedí hranou. Po vyjdení z políčka sa už do neho nemôžu znova vrátiť. Zistite cez koľko najviac políčok vedia prebehnúť, ak:
- vchod je v prvom políčku v prvom riadku a východ v prvom políčku v treťom riadku
- vchod je v prvom políčku v prvom riadku a východ v prvom políčku v druhom riadku.
5. Na papier napísal $6$ modrých za sebou idúcich celých kladných čísel a $6$ žltých za sebou idúcich kladných čísel, pričom najmenšie modré číslo je menšie ako najmenšie žlté číslo. Potom napísal nových $36$ zelených čísel, ktoré vznikli tak, že medzi sebou vynásobí vždy jedno modré číslo s jedných žltým a prejde všetky možné kombinácie (medzi zelenými číslami sa nám môžu čísla aj opakovať). Vieme, že medzi zelenými číslami sa nachádza $49$, že žiadne zelené číslo nie je násobkom čísla $64$ a že medzi zelenými číslami existuje číslo, ktoré je väčšie ako $80$. Aké dvojice čísel môže dostať ako najmenšie modré a najmenšie žlté číslo? Nájdite všetky možnosti.
6. Toto námestie má tvar šesťuholníka. V každom vrchole šesťuholníka stojí dom s kladným celým číslom a medzi každými dvoma susednými domami je na chodníku napísaný súčet čísel týchto dvoch domov. Pre každé číslo od $1$ do $12$ platí, že sa na námestí nachádza práve raz, buď ako číslo domu alebo ako súčet napísaný na chodníku. Ukážte, že ak je vo vrcholoch na domoch napísaných najviac nepárnych čísel ako je celkovo možné, tak v jednom z vrcholov sa určite nachádza dom s číslom $3$.
Vzorové riešenia 1. série nájdeš v časopise Malynar-33-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-33-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 20. november 2023 20:00:00
1. Na obrazci sú dva rovnostranné trojuholníky ako na obrázku. Aká je veľkosť uhla označeného ako $x$?
Tému uhlov ti môže priblížiť aj toto edukačné okienko.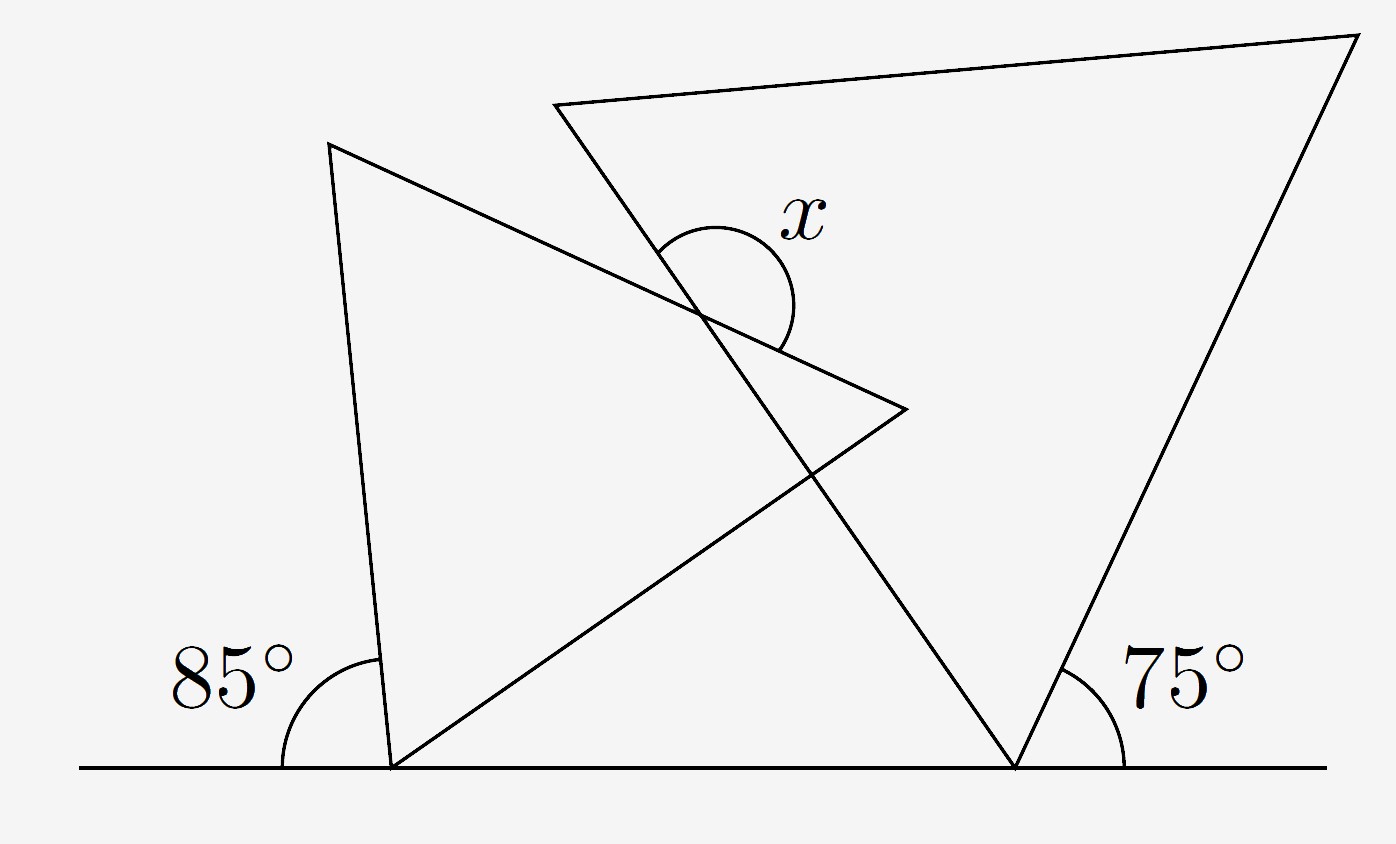
Tému uhlov ti môže priblížiť aj toto edukačné okienko.

2. Deti Anica, Ellie, Robin, John a Zara našli na námestí kamene. Keď si ich podávali a pozerali, zistili, že už nikto nedrží kameň, ktorý našiel. Platia $4$ tvrdenia:
- Robin a Zara našli rovnako veľké kamene.
- Kameň, ktorý našiel John má rovnaký človek, ktorého kameň má John.
- Zara drží kameň, ktorý je menší ako kameň, ktorý našla.
- Robin dostal Anicin kameň.
3. Ukáže im mriežku $1\times100$ políčok. V prvých dvoch políčkach sú položené dve mince. Hru hrajú dvaja hráči, pričom ťah vyzerá tak, že si hráč vyberie jednu z dvoch mincí a posunie ju o ľubovoľný počet políčok doprava. Pri posune nesmie minca preskočiť inú mincu a nesmie byť položená na políčko, kde je práve iná minca. Hra končí, keď sa mince nachádzajú v predposlednom a poslednom políčku mriežky. Vyhráva hráč, ktorý ako posledný urobil ťah. Pre ktorého z hráčov existuje výherná stratégia a aká? Výherná stratégia je postup, podľa ktorého, keď jeden hráč hrá, tak vyhrá bez ohľadu na ťahy súpera.
4. Štvorcová šachovnica s rozmermi $n \times n$ (teda so stranou dlhou $n$ políčok) je zafarbená tak, že každé políčko je buď červené, modré, alebo zelené. Nájdite najmenšie číslo $n$ také, že bez ohľadu na to, ako zafarbíme políčka šachovnice $n \times n$, tak v každom riadku a v každom stĺpci budú nejaké tri políčka rovnakej farby. Ukážte, prečo to pre toto $n$ bude vždy platiť. Tiež ukážte, že pre akékoľvek menšie $n$ vieme šachovnicu $n \times n$ ofarbiť tak, aby v žiadnom stĺpci a v žiadnom riadku neboli tri políčka rovnakej farby.
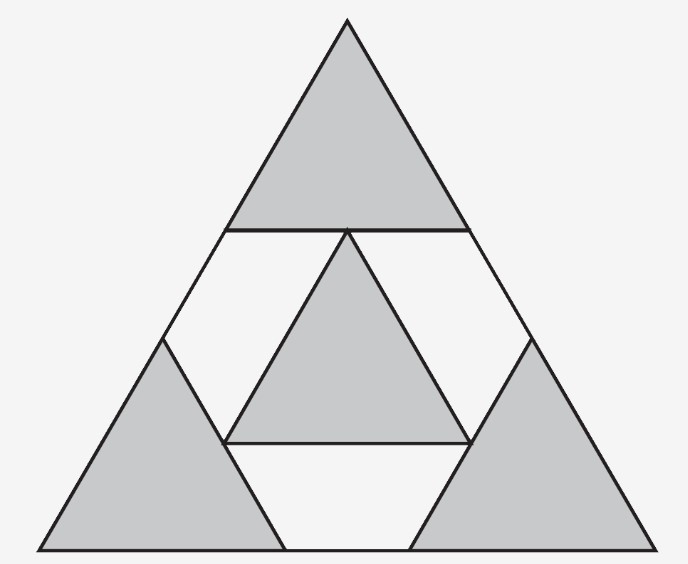
5. Štyri rovnostranné trojuholníky rovnakej veľkosti sú usporiadané vo vnútri väčšieho rovnostranného trojuholníka tak, ako je znázornené na obrázku (vrcholy vnútorného sivého trojuholníka ležia v stredoch strán rohových sivých trojuholníkov). Strany menších trojuholníkov sú rovnobežné so stranami väčšieho trojuholníka. Obsah väčšieho trojuholníka je $50$. Aký je obsah sivej časti?

6. Špeciálny výťah má tri trubice, v ktorých sú guľôčky. Po každej minúte z každej trubice jedna guľôčka zmizne a všetky tri zmiznuté guľôčky sa zjavia v niektorej z týchto trubíc. Ak v nejakej trubici už nie je žiadna guľôčka, objavia sa v každej trubici dve nové guľôčky. Môže nastať situácia, kedy bude vo všetkých troch trubiciach rovnako veľa guľôčok, ak sú na začiatku v trubiciach počty $15$, $20$ a $25$ guľôčok?
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...
Ahoj, máš k nej nejaké konkrétne otázky? Možno by nám pomohli vidieť, s pochopením čoho presne je problém a mohli by sme ti s pochopením zadania lepšie pomôcť.
Je tazko pochopit tu ulohu