
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Malynar, 28. ročník - Zimný semester
Vzorové riešenia 1. série nájdeš v časopise Malynar-28-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-28-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 22. október 2018 20:00:00
1. Čip je v tvare obdĺžnika a skladá sa zo sivých jednotkových štvorcov. Tento obdĺžnik je po obvode kompletne ohraničený vrstvou bielych jednotkových štvorcov. Štvorce sa dotýkajú vždy celou stranou a vrstva má šírku jedného štvorca. Obrázok ukazuje obdĺžnik, ktorý sa skladá z $12$ vnútorných a $18$ vonkajších.
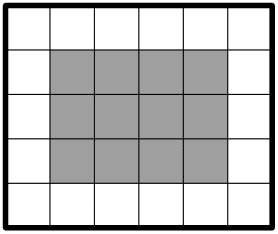
- Nakreslite taký obdĺžnik, ktorý sa skladá zo $6$ vnútorných a $14$ vonkajších štvorcov.
- Rozhodnite, či existuje obdĺžnik, ktorý sa skladá zo $6$ vnútorných a $16$ vonkajších štvorcov.
- Máme obdĺžnik, ktorý je tvorený $20$ vonkajšími štvorcami. Zistite všetky možné počty vnútorných štvorcov, ktoré môžu tvoriť daný obdĺžnik.
- Dokážte, že existuje práve jeden obdĺžnik tvorený $42$ vnútornými štvorcami taký, že počet príslušných vonkajších štvorcov nie je násobkom $5$.
POZOR! Tlačiarenský škriatok zapríčinil, že úloha má vo vašich časopisoch nesprávne zadanie. Správne zadanie nájdete tu a v sekcii časopisy na našej stránke.

2. Dzivé číslo je také štvorciferné číslo, ktorého:
- súčet prvých dvoch číslic je rovnaký ako súčet posledných dvoch číslic,
- súčet krajných dvoch číslic je rovnaký ako vnútorných dvoch číslic.
3. Finále súťaže o najlepšieho robota sa zúčastnili Alex, Laura a Tom. Každý z $22$ porotcov pridelil finalistom $1$, $2$ alebo $3$ body – každému iný počet. $3$ body získal súťažiaci za prvé miesto, $2$ body za druhé miesto a $1$ bod za tretie miesto. Alex získal rovnako veľa prvých a tretích miest. Druhých miest mal o štyri viac než prvých. Laura a Tom získali rovnako veľa prvých miest, avšak druhých miest mala Laura dvakrát viac než Tom. Kto vyhral finále? Koľko získal bodov?
4. Máme tabuľku s výrezom v tvare obráteného Z (obrázok), ktorá má túto vlastnosť: keď zakrúžkujeme ľubovoľných päť čísel tak, že v každom stĺpci aj v každom riadku je zakrúžkované práve jedno, a sčítame ich, vždy dostaneme rovnaký súčet. Doplňte čísla na prázdne (biele) miesta. Nájdite všetky riešenia.


5. Niekoľko ostrovov je pospájaných mostami, pričom medzi dvomi ostrovmi vedie najviac jeden most. Navyše, z rôznych ostrovov vychádza rôzny počet mostov (ak z nejakého ostrova vychádza jeden most, z ostatných ostrovov musí vychádzať $0$ mostov alebo aspoň $2$ mosty). Dokážte, že bez ohľadu na to, ako sú ostrovy poprepájané, tak nie je možné splniť dané podmienky.
- Riešte pre prípad, že ostrovov je $7$.
- Riešte pre prípad, že ostrovov je viac ako $7$ – nájdite všeobecné riešenie pre všetky také počty.
POZOR! Tlačiarenský škriatok zapríčinil, že úloha má vo vašich časopisoch nesprávne zadanie. Správne zadanie nájdete tu a v sekcii časopisy na našej stránke.
6. Strecha má tvar štvorca $ABCD$. Heliport je v tvare sivého trojuholníka. Akú časť plochy strechy tvorí heliport? Úlohu riešte bez použitia rysovacích pomôcok a merania vzdialeností.
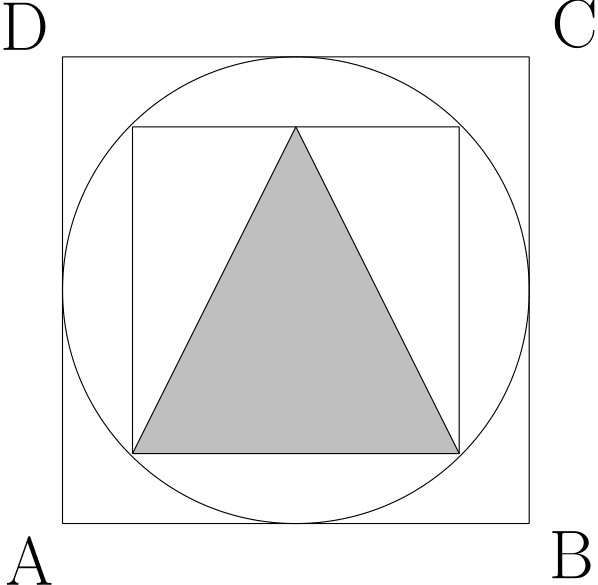

Vzorové riešenia 1. série nájdeš v časopise Malynar-28-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-28-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Pozri sa na pár tipov, ktoré ti pomôžu pri riešení.
Termín série: 26. november 2018 20:00:00
1. Štyri roboty sa nachádzajú na priamke a predstavujú body $P$, $Q$, $R$ a $S$ v nejakom poradí. Vieme, že dĺžky úsečiek $|PQ|$, $|QR|$, $|RS|$ a $|SP|$ sú jednotlivo $13$, $11$, $14$ a $12$. Aké je poradie bodov na priamke a aká je vzdialenosť medzi bodmi, ktoré sú od seba najvzdialenejšie? Nezabudnite nájsť všetky možnosti.
2. Les má podobu štvorcovej tabuľky o rozmeroch $n\times n$, ktorá je vyplnená všetkými číslami od $1$ po $n\cdot n$ tak, že čísla v každom riadku, každom stĺpci a aj na oboch hlavných uhlopriečkach majú rôzne súčty. Aká najmenšia tabuľka sa dá zostrojiť? Prečo sa menšia už zostrojiť nedá? (Ak ste sa s tým ešte nestretli, tak $n$ označuje nejaké neznáme číslo. Ak by bolo napr. $n=4$, tak ide o tabuľku so $4$ riadkami a $4$ stĺpcami, kde nájdeme čísla od $1$ do $4\cdot4$, teda do $16$.)
3. V obávanom bludisku sa nachádza portál pod jedným z polí $\alpha$ (alfa), $\beta$ (beta), $\gamma$ (gama), $\delta$ (delta), $\omega$ (omega). Každé pole sa nachádza na inom mieste (viď obrázok). Len pod jedným poľom sa nachádza portál a môžeme sa dostať len pod jedno zvolené pole. V okolí obávaného bludiska sa pohybovalo $5$ strážcov, každý o portáli tvrdil niečo iné. Postupne títo piati ľudia povedali:
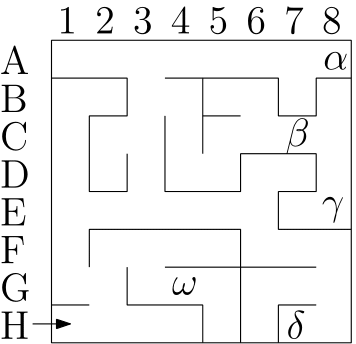
- Na najkratšej ceste za portálom sa musíš aspoň štyrikrát otočiť doprava.
- Portál sa nachádza v riadku označenom písmenom zapisujúcim spoluhlásku.
- Na najkratšej ceste za portálom musíš prejsť aspoň cez $15$ políčok.
- Portál sa nachádza na políčku, ktoré je v stĺpci označenom párnym číslom.
- Na najkratšej ceste za portálom sa musíš aspoň štyrikrát otočiť doľava.

4. Hráč $A$ a Hráč $B$ majú na papieri napísaných $100$ jednotiek oddelených medzerami. Hráč $A$ začína a s Hráčom $B$ sa ťah po ťahu striedajú. Každý hráč musí v každom ťahu umiestniť medzi nejaké dve susedné jednotky znamienko plus alebo znamienko krát. Po vyplnení všetkých medzier ostane na papieri príklad, ktorého výsledok je buď párny, alebo nepárny. Ak je párny, vyhráva Hráč $A$, ak je nepárny, vyhráva Hráč $B$. Jeden z hráčov dokáže hrať tak, aby vždy vyhral, a to bez ohľadu na súperove ťahy. Ktorý z hráčov to je a prečo?
5. Okolo okrúhleho stola je v pravidelných rozostupoch rozostavených pätnásť stoličiek. Na stole sú kartičky s menami pätnástich hostí. Hostia si všimli kartičky až keď si už sadli. A tak sa stalo, že nikto z pätnástich hostí nesedel pred svojou vlastnou kartičkou. Dokážte, že je možné otočiť stôl tak, aby aspoň dvaja hostia sedeli na správnych miestach.
6. Koľko rôznych sedempísmenových „slov“ vieme vytvoriť z písmen $A$, $B$, $C$, $D$? „Slovo“ je ľubovoľný zhluk abecedne zoradených písmen - napríklad $AAAABBD$ je „slovo“ ale $AACCBDA$ nie je. „Slová“ sú rovnaké len vtedy, ak sa zhodujú písmená na všetkých ich pozíciách. V „slove“ nemusíme použiť každé zo štyroch písmen.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...